
Tibetischer Abakus mit losen Steinen (rde´u-rtsis)
Der tibetische Abakus mit losen Steinen (rde'u-rtsis) ist ein Rechenhilfsmittel zur Durchführung von Rechenaufgaben und insbesondere von Umrechnungen von Größenangaben unterschiedlicher Maße und Gewichte.
Er wurde ausschließlich in den für Steuereinnahmen zuständigen Stellen der Verwaltung der zentraltibetischen Regierung oder in den Schatzämtern großer tibetischer Klöster bis zum Jahre 1959 verwendet.
Zur Durchführung von Rechnungen mit dem Abakus mit losen Steinen gab es verschiedene Lehrbücher. Das älteste bekannte Lehrbuch dieser Art wurde von Düchungpa ('Dus-byung-pa) Ananda im 17. Jahrhundert verfasst. Die Verwendung des Abakus mit losen Steinen geht offensichtlich auf die Zeit der Tibetischen Monarchie (7. – 9. Jahrhundert) zurück.
Für Rechenaufgaben in anderen Bereichen, insbesondere in der tibetischen Kalenderrechnung und der tibetischen Astronomie, wurde ein anderes Rechenhilfsmittel verwendet, der tibetische Sandabakus, auch tibetisches Sandrechenbrett genannt.
Inhaltsverzeichnis
1. Das Rechengerät
2. Addition und Subtraktion
3. Umrechnungen
3.1. Rechnen mit Brüchen (zur-rtsis)
3.2. Das Rechnen mit dem "Gehen" (´gro) genannten Umrechnungsverfahren
3.3. „Verkettung von Steinmengen“ (sngon-ma´i cha-´gros)
3.4. Differenzbetragsrechnung mittels Zinsaufschlags- und Zinsabschlagssätzen für Darlehen
4. Literatur

1. Das Rechengerät
Grundlage der Rechenoperationen waren Reihen von Steinen, die vor der rechnenden Person von links nach rechts, also horizontal, entweder auf der ebenen Erde, auf einem Tisch oder einem speziellen Rechenbrett niedergelegt wurden. Das Rechenbrett war manchmal mit Linien in Felder aufgeteilt, um die einzelnen Größen leichter unterscheiden zu können. Die Reihen repräsentieren Stellenwerte, wobei keine dieser Steinchenreihen mehr als 9 Einheiten umfasste. Die Steinreihen wurden übereinander platziert.
Mengenangaben waren grundsätzlich Messgrößen für Naturalien oder Geld, wie z.B. Getreide, Gold, Silber oder Heu nach traditionellen Maßeinheiten.
Für Getreide wurde ein Volumenmaß verwendet. Die größte Maßeinheit war hier ein khal, welches ungefähr 18 Liter umfasste. Ein khal umfasste 20 bre. Ein bre umfasste 6 phul (eine Hand voll). Ein phul wurde wiederum in 120 sogenannte "Innere Stücke" (nang gi rdog-ma) unterteilt. Die letztgenannte Größenangabe hatte keine praktische Bedeutung und diente nur der Kalkulation zur Vermeidung von Resten.
Als Rechensteine wurden verwendet: Aprikosenkerne (kham-tshig), Porzellanscherben (dkar-yog), schwarze Steine (rdel-nag), Bohnen (rgya-sran), Zehnerhölzer (bcu-shing), halbe Aprikosenkerne (kham-tshig phyed) und weiße Steine (rdel-dkar).
Beispiel für die Darstellung einer Zahlgröße: Die Größe einer Getreidemenge sei mit 537694 khal, 19 bre, 5 phul und 97 nang gi rdog-ma angegeben. Dies ergibt auf dem Abakus mit losen Steinen folgendes Bild:
 |
Darstellung von 537694 khal, 19 bre, 5 phul und 97 nang gi rdog-ma |
2. Addition und Subtraktion
Für die Addition von Zahlen wird beim Rechnen mit dem Abakus das Wort „Gehen“ ('gro) verwendet. Damit wird ausgedrückt, dass beim Addieren Steine aus einer ungeordneten Menge einer geordneten Menge hinzugefügt werden, also gleichsam von einer Menge zur anderen „gehen“. Für die Durchführung der Addition ist wesentlich, dass in einer horizontalen Reihe niemals mehr als neun Steine platziert sein dürfen. Dies führt regelmäßig dazu, dass der Rechnende zunächst die vorhandene Menge reduziert, um dann entsprechend größere Beträge hinzuzufügen. Die Durchführung der Rechenoperationen wird regelmäßig durch einen Gesang begleitet, in dem der Rechenmeister sich selbst vorträgt, was er gerade durchführt.
Beispiel: Addiere zu 189 den Betrag von 9•7 = 63.
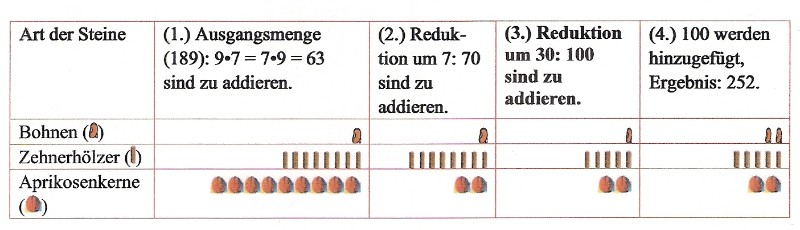 |
Addition von 189 + 63 |
Bei dieser Rechnung wird folgender Text singend vorgetragen:
„(1.) Sieben mal neun (oder) neun mal sieben, also dreiundsechzig, haben eben genau zu gehen. (2.) Mit dem Geben von 3, 6, 7 auf dreiundsechzig sind es siebzig. (3.) Siebzig sagend, sind es mit dem Geben von dreißig nun einhundert, die eben genau zu gehen haben. (4.) Einhundert also sind gegangen.“
Während bei der Addition durch Wegnahmen von der Grundmenge der zu addierende Betrag in der Regel erhöht wird, ergibt sich bei der Subtraktion ('then; „abziehen“) durch die Subtraktion höherer Beträge zumeist eine anschließende Addition des zuviel weggenommen Betrages.
Beispiel: Subtrahiere von 243 den Betrag von 9•8 = 72.
 |
Subtrahiere von 243 den Betrag von 9•8 = 72 |
Bei dieser Rechnung wird folgender Text singend vorgetragen:
„(1.) Acht mal neun (oder) neun mal acht, also 72 sind eben genau abzuziehen. (2.) Mit dem Abziehen der 70 von hundert sind es genau dreißig, die eben genau zurückzugehen haben. (3.) Dreißig sind also zurückgegangen. (4.) Zwei sind eben genau abzuziehen. Zwei also sind abgezogen.“
3. Umrechnungen
Eine der Hauptaufgaben der tibetischen Finanzbehörden war das Umrechnen von Größenangaben insbesondere für bestimmte Getreidemengen, die mit lokalen Messgeräten gemessen worden waren. Dabei ist zu beachten, dass die Hauptmasse der Steuereinnahmen in Tibet aus abgeliefertem Getreide bestand. Diese Getreide wurde in Vorratshäusern dezentral gelagert und die ein-. und abgehenden Mengen der Finanzbehörde gemeldet. Zwar verwendeten die für die Finanzen zuständigen Behörden, wie oben beschrieben, eine Normgröße für ein khal Getreide, welche mit einem Normmessgerät ermittelt wurde. Jedoch wurde in den verschiedenen Landesteilen Tibets eine Vielzahl unterschiedlich großer Messgeräte verwendet.
Die Aufgabenstellung lässt sich wie folgt beschreiben: Gemeldet wurde der Zugang einer Getreidemenge M1, welche mit einem Messgerät gemessen wurde, dessen Größe im Verhältnis zum Normmessgerät nicht 20 bre, sondern y1 bre betrug. Hierbei ist y1 also ungleich 20. Die Fragestellung lautet: Wie groß ist diese Getreidemenge M1, wenn sie mit dem Normmessgerät gemessen wird? Hierbei verstanden die tibetischen Mathematiker y1 als Anteil oder Teil von einem khal bzw. von 20 bre, also y1 = 10 bre als die Hälfte von einem khal bzw. y1 = 5 bre als ¼ von einem khal. Wenn also M1 mit einem Messgerät der Größe ¼ khal ermittelt wurde, dann konnte M nur ¼ vom M1 sein.
Die Umrechnungsverfahren von Größenangaben bestimmter Getreidemengen waren kein arithmetisches Rechnen mit Zahlen, sondern Transformationen von Mengen. Dabei waren die Darstellungen mit Steinen eigentlich Abbildungen vorgegebener Getreidemengen. Vorgegeben waren die Ausgangsmengen in einer Niederschrift mit Ziffern. Gleichermaßen wurde das Ergebnis der Umrechnung wieder in Listen mit Zahlzeichen festgehalten.
Die wichtigsten dieser Umrechnungsverfahren, wurden von ´Dus-byung-pa als zur „Brüche“, ´gro „Gehen“, sngon-ma´i cha-´gros „Verkettung von Steinmengen“, ngo-thog spor-gcog „Aufschlagen und Abziehen mit der direkten Differenz“ und ´bun gyi spor-gcog „Differenzbetragsrechnung mittels Zinsaufschlag- und Zinsabschlagsätzen für Darlehen“ bezeichnet.
3.1. Rechnen mit Brüchen (zur-rtsis)
Die unterschiedliche Größe von örtlichen Messgeräten wurde von ´Dus-byung-pa in einer Liste als Brüche dargestellt. Diese bildeten die Grundlage für eine praktische Umrechnung vorgegebener Größenangaben. Das praktische Verfahren der Umrechnung sei an einem Beispiel erläutert. Vorgegeben sei die Größenangabe einer Getreidemenge als 159 khal, 18 bre und 4 1/3 phul. Deren Größe wurde mit einem Messgerät von 18 bre ermittelt. Dazu platziert man die Ausgangsmenge in Steinen, wobei man die nang gi rdog-ma für 1/3 phul neben die Steine für phul platziert. In die Mitte platziert man 18 bre als Gedächtnisstütze für die Größe des lokalen Messgerätes. Nach der Liste des ´Dus-byung-pa sind 18 bre gleich 9/10 khal.
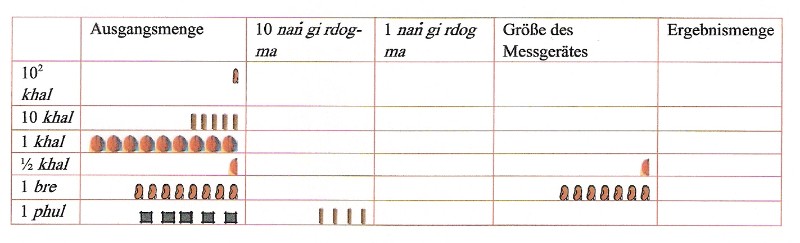 |
Ausgangssituation bei der Umrechnung mit Brüchen |
Im ersten Schritt wird festgestellt, dass 9/10 von 100 gleich 90 sind. Entsprechend wird die Ausgangsmenge um 100 reduziert und in der Ergebnismenge 90 platziert mit folgendem Ergebnis:
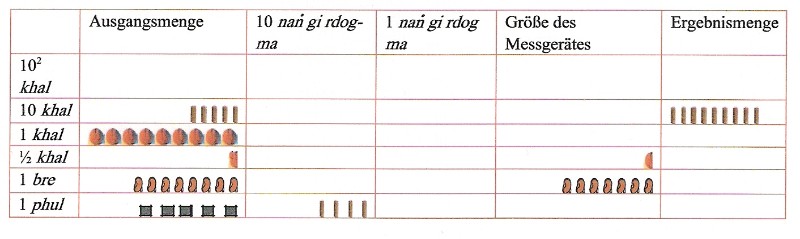
Bei dieser Rechnung wird folgender Text singend vorgetragen:
„Achtzehn bre (bezogen) auf ein khal sind neun Zehntel. Von zehn wird zu neun übergegangen. Falls sich zehn ergeben sind es neun. Falls sich hundert ergeben, sind es neunzig. Im Unterschied zu hundert khal sind es genau neunzig khal. Dreißig, sechzig, neunzig also sind gegangen.“
Im nächsten Schritt wird festgestellt, dass 9/10 von 10 gleich 9 ist, also folglich 9/10 von 50 = 5•10 gleich 5•9 = 45 ist. Also sind zu der Ergebnismenge 45 zu addieren, wobei die Addition nach dem oben beschriebenen Verfahren durchgeführt wird. Dies ergibt folgendes Ergebnis:
 |
2. Schritt bei der Rechnung mit Brüchen |
Bei dieser Rechnung wird wiederum der entsprechende Text singend vorgetragen, auf dessen Wiederholung hier verzichtet wird.
Als letztes sein hier noch auf die Umrechnung von 9 khal und ½ khal eingegangen. Nach Umrechnung von 9 ½ khal in bre erhält man 190 bre. Von dem Teilbetrag von 100 ermittelt man 9/10 gleich 90. Diese rechnet man im Kopf auf 4 ½ khal um und addiert dies man zu Ergebnismenge:
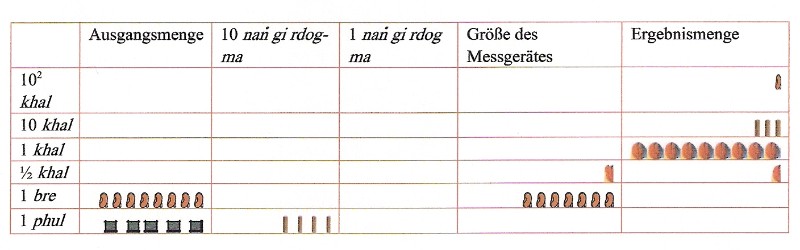
Von den 190 bre sind nun noch 90 bre umzurechnen. Hierzu ermittelt man durch Kopfrechnen, dass 81 bre zur Zielmenge zu addieren sind. Dies entspricht 4 khal und 1 bre. Die Addition ergibt dann folgendes Ergebnis:
 |
4. Schritt bei der Rechnung mit Brüchen |
Das weitere Verfahren wird analog fortgesetzt.
3.2. Das Rechnen mit dem "Gehen" (´gro) genannten Umrechnungsverfahren
Das sogenannte Rechnen mit dem „Gehen“ genannten Verfahren hat ´Dus-byung-pa nach seinen eigenen Aussagen selbst erfunden. Es unterscheidet sich in der praktischen Ausführung nicht von der vorstehend beschriebenen Umrechnung mit Brüchen, beinhaltet aber ein anderes Verständnis für die Umrechnung, das ´Dus-byung-pa wie folgt formuliert: Wenn der lokale Messkasten anstelle von 20 bre nur 8 bre fasst, bedeutet dies, das jeweils statt 20 bre bzw. 20 khal der gemeldeten Menge tatsächlich nur 8 bre bzw. 8 khal nach dem Normalmaß vorliegen. Dies bedeutet, dass man von 20 bre bzw. 20 khal der Ausgangsmenge zu 8 bre bzw. 8 khal der Zielmenge „überzugehen“ hat. Verkürzt ist dies gleichbedeutend mit einem „Gehen“ von zehn zu vier.
Als Beispiel für dieses Verfahren sei hier die Umrechnung von einer Getreidemenge von 14 khal, 19 bre, 1 phul und 30 nang gi rdog-ma, die mit einem Messgerät der Größe von 6 bre gemessen wurde, erläutert. Der Rezitationstext mit der detaillierten Durchführung ist auf S. 742f zu finden. Das Umrechnungsverfahren wurde nachfolgend verkürzt dargestellt.
Umrechnungsverfahren „Gehen“ von einer Getreidemenge von 14 khal, 19 bre, 1 phul und 30 nang gi rdog-ma, die mit einem Messgerät der Größe von 6 bre gemessen wurde:
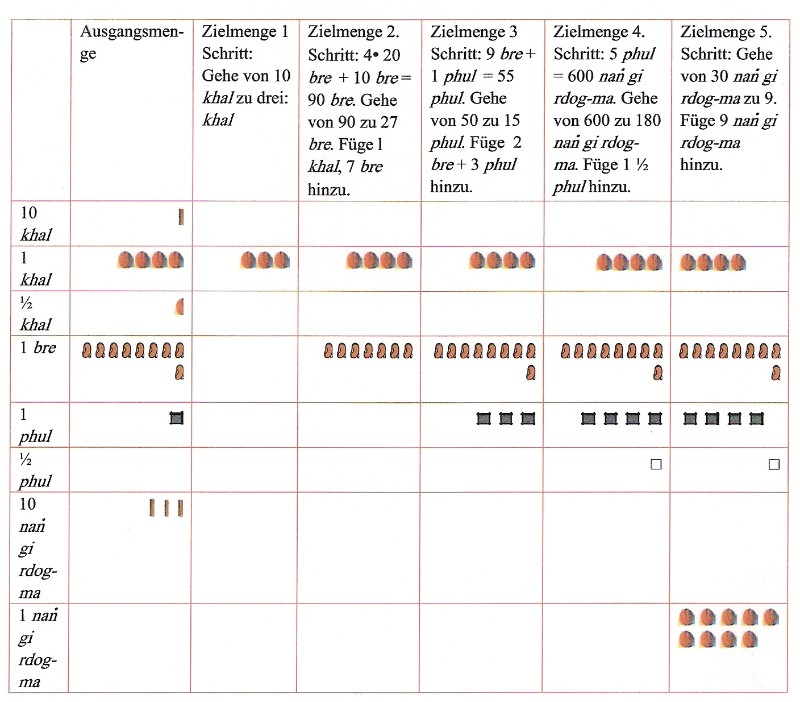 |
Umrechnung mit dem Gehen genannten Verfahren |
3.3. „Verkettung von Steinmengen“ (sngon-ma´i cha-´gros)
Umrechnung eines als Steinchenmenge niedergelegten Gesamtbetrages durch sukzessives Ausrechnen von miteinander verbundenen Teilbeträgen (sngon ma'i cha 'gros; „Gehen unter Orientierung an vorausgegangenen Teilbeträgen“), die anschließend addiert werden.
Formelmäßig lässt sich dies wie folgt darstellen: Ist M der Ausgangsbetrag, MN der zu errechnende Betrag, V das Verhältnis (Bruch) der Größe des lokalen Messgerätes zum Normmessgerät (20 khal), und sind x, y, und z unterschiedliche Brüche, so lautet die Rechenvorschrift MN = M•x + (M•x)•y + (M•x•y)•z. Dabei muß V = x + x•y + x•y•z gelten.
Man rechnet also ausgehend von M mit M•x=M1 zunächst einen Teilbetrag M1 aus, der als Steinchenmenge rechts neben M platziert wird.
Aus dieser Ergebnismenge errechnet man eine zweite Steinchenmenge mit M1•y=M2, welche rechts neben M1 platziert wird.
Aus M2 erstellt man eine weitere Steinmenge durch M2•z, welches man rechts neben M2 platziert. Das Ergebnis sind vier Steinchenmengen, nämlich
M, (M•x), (M•x•y), (M•x•y•z)
oder
M, M1, M2, M3.
Das Umrechnungsergebnis ergibt sich dann durch
M1 + M2 + M3.
Mit Zahlen ausgedrückt z.B.:

Das Ergebnis der Umrechnung ergibt sich aus dem Zusammenlegen (Addition) der drei errechneten Steinchenmengen, also:

Beispiel:
Beträgt die Größe eines örtlichen Messgerätes 1 bre, 1 phul und 1/3 phul des Normalmaßes, so rechnet man die mit dem örtlichen Messgerät ermittelte Gesamtmenge M mit dem Bruch
x = 1⁄20 um:
M1 = M•x = M•1⁄20.
Das Ergebnis M1 rechnet man mit dem Bruch y = 1⁄6 um:
M2 = M1•y = M1•1⁄6.
Dieses Ergebnis M2 wiederum rechnet man mit dem Bruch z = 1⁄3 um:
M3=M2•1⁄3.
Das Ergebnis der Gesamtrechnung ergibt sich durch die Addition dieser drei Teilbeträge M1, M2 und M3.
Grundlage dieser Umrechnungsmethode ist das Zerlegen von Brüchen. Im vorstehenden Beispiel ist nämlich das Größenverhältnis des örtlichen Messgerätes zum Normmessgerät
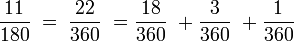 .
.
Dies ist wiederum

Entsprechend dem vorstehenden Beispiel sei die Ausgangsmenge 720 khal, gemessen mit dem lokalen Messgerät.
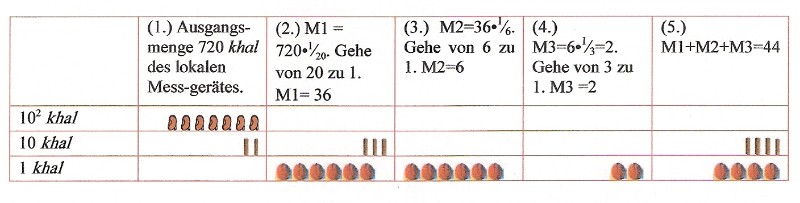 |
Umrechnung mit der Verkettung von Steinmengen |
3.4. Differenzbetragsrechnung mittels Zinsaufschlags- und Zinsabschlagssätzen für Darlehen
Bei diesem Umrechnungsverfahren findet eine den tibetischen Mathematikern geläufige Methode der Zinseszinsberechnung Anwendung. Dabei bezeichnet ´bun sowohl den zuzüglich Zinsen und Zinseszins geschuldeten Darlehensbetrag als auch den Zinssatz. Hierbei werden zwei unterschiedliche Methoden der Berechnung von Schulden unterschieden, nämlich die dbus-´bun (zentraltibetischer Zinssatz: "Bei Zweien kommt Einer als Zins hinzu" = 50 % Zinsen) und die gtsang-´bun (Zinssatz für die Region gTsang: "Bei Dreien kommt Einer als Zins hinzu" = 33 1⁄3 % Zinsen).
Ausgangspunkt ist in der Regel die Berechnung des ursprünglichen geschuldeten Darlehensbetrages unter Verzicht auf die Zinsen für ein Jahr oder mehrere Jahre. Dabei werden die jährlich angefallenen Zinsen berechnet und sukzessiv vom Schuldbetrag abgezogen.
Dazu multipliziert man den Betrag, der den aktuellen Schuldenstand ausmacht, bei dem dbus-´bun genannten Zinssatz für ein Jahr mit 1⁄3 (dbus-´bun gcig-bcag "Reduzierung um den Zinssatz Zentraltibets für ein Jahr") und zieht das Ergebnis von der Ausgangsmenge ab, was einer Multiplikation mit 2⁄3 entspricht. Für zwei Jahre wird dies ausgehend vom zuvor errechneten Schuldbetrag wiederholt (dbus-´bun gnyis-bcag "Reduzierung um den Zinssatz Zentraltibets für zwei Jahre") und für ein eventuelles drittes Jahr wird dies dann noch einmal durchgeführt (dbus-´bun gsum-bcag "Reduzierung um den Zinssatz Zentraltibets für drei Jahre"). Bei dem Zinssatz der Provinz gTsang (tib.: gtsang-´bun) rechnet man nicht mit dem Bruch 1⁄3 sondern mit 1⁄4.
Für die Umrechnung der Größen von Getreidemengen ist dieses Verfahren dann z. B. anwendbar, wenn die Größe des lokalen Messgerätes oder die Differenz dieses Betrages zu einem khal des Normaßes einem in der Zinseszinnsrechnung auftretenden Bruch entspricht. Z. B. entspricht 3⁄4• 3⁄4• 3⁄4 der Maßgröße 8 bre + 2 phul + 1⁄2 + 1⁄8 phul und 2⁄3•2⁄3 entspricht der Maßgröße 8 bre + 5 phul + 1⁄3 phul.
Beispiel:
Das örtliche Messgerät fasst 1 khal, 8 bre, 5 phul und 1⁄3 phul des Normalmaßes (1 khal oder 20 bre, gemessen mit dem gtan-tshigs mkhar-ru). Der Gesamtbetrag (M), der mit dem örtlichen Messgerät ermittelt wurde, wird zweimal platziert. Der zweitplazierte Betrag wird mit zweifachem Zinsabschlag reduziert. Tibetisch sukzessive gerechnet bedeutet dies MD1 = M – M•1⁄3, MD2 = MD1 – MD1•1⁄3. Direkt gerechnet: MD2 = M•2⁄3•2⁄3. Dies ergibt den Unterschiedsbetrag. Dieser Unterschiedsbetrag MD2 wird zu dem erstplazierten Betrag M addiert.
Verifikation: Die Differenz zwischen der Größe des lokalen Messgerätes und dem Normalmaß beträgt 8 bre, 5 phul und 1⁄3 phul. Zur Probe wird mit M = 1 khal gerechnet. Dies ergibt 1•2⁄3•2⁄3 = 4⁄9 khal = 80⁄9 bre = 8 bre + 8⁄9 bre = 8 bre + 48⁄9 phul = 8 bre + 5 phul + 3⁄9 phul = 8 bre + 5 phul + 1⁄3 phul.
4. Literatur
Dieter Schuh: Studien zur Geschichte der Mathematik und Astronomie in Tibet, Teil 1, Elementare Arithmetik. Zentralasiatische Studien des Seminars für Sprach- und Kulturwissenschaft Zentralasiens der Universität Bonn, 4, 1970, S. 81–181
'Dus byung pa Ananda: mKhas dbang 'dus byung pa'i rde'u'i rtsis gzhung sarga brgyad la dag ther byas pa rab sbyangs gser gyi me long. Tibetischer Blockdruck (17. Jahrhundert), 16 Blatt und 4 Bl. Tabellen. (Grundwerk des´Dus byung pa Ananda über das Rechnen mit dem Abakus mit losen Steinen. Das wichtigste bisher bekannt gewordene Lehrbuch über das Rechnen mit diesem Abakus, verfasst im 17. Jahrhundert)
Ngag dbang chos 'byor: mKhas dbang 'dus 'byung pas mdzad pa'i rdel-rtsis gzhung sarga brgyad kyi zab gnas sgo brgya 'byed pa'i 'grel bshad dper brjod 'phrul gyi lde-mig. Tibetischer Blockdruck (18. Jahrhundert), 48 Blatt. (Kommentar zum Rab sbyangs gser gyi me long des 'Dus byung pa Ananda über das Rechnen mit dem Abakus mit losen Steinen)
Autor: Dieter Schuh, 2010





