Mengen kann man auf alle erdenkliche Art bilden, wie z. B. die Menge aller Trommeln (M2), die Menge aller Musikinstrumente (M1), die Menge aller vom Menschen hergestellten Gegenstände (M). Grundvoraussetzung solcher Mengenbildung ist die Unterscheidbarkeit der Dinge, die als Elemente (m) zu einer Menge (M) zusammengefasst werden. Diese ergibt sich aus unterschiedlichen Eigenschaften, wie z. B. grün, gelb und rot. Natürlich lassen sich auch Eigenschaften zu Mengen zusammenfassen. Der von Cantor verwendete Begriff der Teilmengen lässt sich am Beispiel der vorstehend genannten Mengen verdeutlichen. Die Menge der Trommeln (M2) ist eine Teilmenge der Menge der Musikinstrumente (M1). Die Menge der Musikinstrumente (M1) ist eine Teilmenge der Menge der vom Menschen hergestellten Gegenstände (M). In der Formelsprache der Mathematik wird dies mit dem Zeichen ⊂ dargestellt, so dass wir statt „Die Menge der Trommeln (M2) ist eine Teilmenge der Menge der Musikinstrumente (M1)“ auch M2 ⊂ M1 und anstelle von „Die Menge der Musikinstrumente (M1) ist eine Teilmenge der Menge der vom Menschen hergestellten Gegenstände (M)“ auch M2 ⊂ M schreiben können. Die von Cantor oben aufgeführte Relation der Teilmengen besagt dann auch, dass „Die Menge der Trommeln (M2) ist eine Teilmenge der Menge der vom Menschen hergestellten Gegenstände (M)“, also M2 ⊂ M, gilt. Bildlich dargestellt ist dies in der Abbildung 2.
In diesem Zusammenhang ist ein weiterer Begriff von Bedeutung, nämlich der der sogenannten Komplementärmenge. Damit ist die Menge (MC) der Elemente gemeint, die nicht zu einer bestimmten Menge M gehört. Dies lässt sich mit der folgenden Zeichnung verdeutlichen:
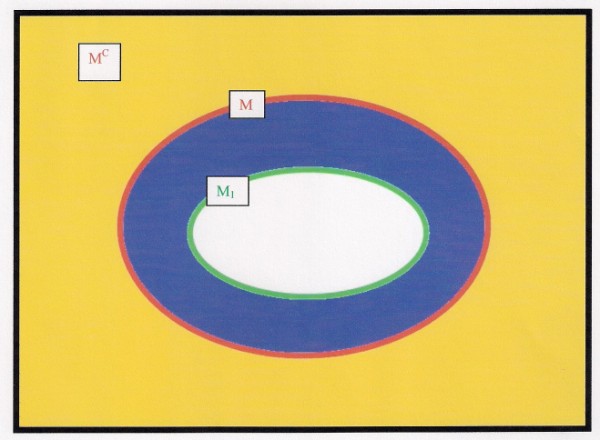 |
Abbildung 5 |
Verstehen wir unter der Menge M die Menge der der Gegenstände, die innerhalb des rot umrandeten Bereichs liegen, so wird die Komplementärmenge MC, also die Menge der Gegenstände, die nicht zu M gehören, von den Objekten gebildet, die in dem gelb markierten Bereich liegen. Die oben dargestellte Menge M1 (Menge der Objekte innerhalb der grünen Linie) ist eine Teilmenge von M. Die Komplementärmenge von M1, also M1C, wird von den Elementen gebildet, die sich außerhalb der grünen Linie und somit im blau und gelb markierten Bereich befinden.
4. Begriffe der Mengenlehre in der tibetischen Logik
Für die Elemente (m) einer Menge gilt: Ist m eine Element der Menge M (was mit m ∊ M umschrieben wird), so ist m natürlich kein Element der Komplementärmenge MC von M (was mit m ∉ MC geschrieben wird). Die Begriffe Menge und Komplementärmenge finden sich auch in der tibetischen Logik mit den Bezeichnungen mthun-phyogs (= Menge bzw. Gesamtheit von Objekten mit einer bestimmten Eigenschaft) und mi-mthun-phyogs (= Komplementärmenge bzw. Gesamtheit der Objekte, die eine bestimmte Eigenschaft nicht haben). Definiert werden diese Begriffe anhand von Beispielen.
So wird die mthun-phyogs (Menge M) der Objekte, die die Eigenschaft „unbeständig“ (mi-rtag-pa) haben, als Gesamtheit der Objekte definiert, die die Eigenschaft „unbeständig“ nicht nicht-haben (mi-rtag-pas mi-stong-pa). Diese Menge (mthun-phyogs) umfasst somit alles, welches die Eigenschaft „unbeständig“ hat bzw. unbeständig ist (mi-rtag-pa yin pa).
Die mi-mthun-phyogs (Komplementärmenge MC) der Objekte, die die Eigenschaft „unbeständig“ (mi-rtag-pa) haben, wird als Gesamtheit der Objekte definiert, die die Eigenschaft „unbeständig“ nicht haben (mi-rtag-pas stong-pa).
Die Bildung von Mengen (mthun-phyogs) ist dadurch möglich, dass man in ihnen Elemente nach gemeinsamen, klar verständlichen Eigenschaften zusammenfasst. So umfasst die Menge aller Geraden Zahlen (MG) zunächst ausschließlich natürliche Zahlen und davon insbesondere nur die Zahlen, die ohne Rest durch zwei teilbar sind. Diese Eigenschaft (chos), „ohne Rest durch zwei teilbar zu sein“, kommt allen Elementen (mg) zu, die zur Menge der Geraden Zahlen gehören. Anders gesprochen ist mg nur dann Element der Menge der Geraden Zahlen, wenn es eine gerade Zahl ist. Diese Eigenschaft ist gleichsam konstitutiv für die Bildung der Menge (mthun-phyogs) MG.
Grundlage meiner hier vorgelegten Betrachtungen ist die These, dass der Inhalt der gesamten tibetischen Logik strukturell auf den oben zitierten Satz von Cantor, nämlich „Ist M2 ein Theil von M1, M1 ein Theil von M, so ist auch M2 ein Theil von M.“ reduziert werden kann, und dass die tibetischen Logiker in der Anwendung auf konkrete Sachverhalte bzw. konkrete Mengen nur die Bedingungen untersuchen, unter denen diese Aussage Gültigkeit hat. Dies bedeutet, dass die tibetische Logik im Prinzip nur versucht, die Bedingungen für konkrete Fälle zu formulieren, nach denen M2 ⊂ M1 und M1 ⊂ M wahr ist, woraus M2 ⊂ M als unbestreitbar wahr resultiert. Aus der Sicht der tibetischen Logik steht für die Verifizierung von M2 ⊂ M1 und M1 ⊂ M die Menge M1 im Mittelpunkt der Analyse. Wir würden aus dieser Sicht fragen: Ist M1 Obermenge von M2? Ist M1 Untermenge von M? Wenn beide Fragen mit „Ja“ beantwortet werden gilt: M2 ⊂ M.
Das Mengenverhältnis M2 ⊂ M1 veranlasst mich, zunächst einen Blick auf die Elemente m1 der Menge M1, die ich hier als Obermenge bezeichne, und die Element m2 der Teilmenge bzw. Untermenge M2 zu werfen.
M1 ist nur dann Obermenge von M2 (M1 ⊃ M2), wenn die Elemente m2 der Menge M2 auch Elemente der Menge M1 sind. Nehmen wir hierzu als Beispiel wiederum die Menge der Natürlichen Zahlen (MN), also {1,2,3,…} und die Menge der Geraden Zahlen (MG), so wird die Menge der Natürlichen Zahlen dadurch gebildet, dass diese aus den Zahlen 1,2,3,… besteht. Die Menge der Geraden Zahlen MG ist natürlich nur dann Teilmenge der Menge der Natürlichen Zahlen, wenn die Elemente der Menge der Geraden Zahlen auch die Eigenschaft „Natürliche Zahlen zu sein“ haben. Aus der Sicht der Obermenge (Natürliche Zahlen) müssen die Elemente der Untermenge (Gerade Zahlen) also alle die für die Obermenge konstitutive Eigenschaft (chos) haben, nämlich „Natürliche Zahlen zu sein“. Insofern sollte man phyogs-chos als „eine allen Elementen einer Menge (phyogs) gemeinsame Eigenschaft (chos)“ übersetzen.
Betrachtet man zum Beispiel die Menge der Trommeln (M2) und die Menge der Musikinstrumente (M1). Aus der Sicht der Menge der „Musikinstrumente“ ist diese Menge nur dann Obermenge der Menge der Trommeln, wenn alle Trommeln (phyogs) die M1 konstituierende oder bildende Eigenschaft (chos) „Musikinstrument sein“ auch haben.
Das Vorhandensein der für die Obermenge M1 konstitutiven Eigenschaft in den Elementen der Untermenge M2 wird auch im Tibetischen umständlich wie folgt beschrieben: ´god tshul dang mthun pa nyid du nges-pa „es ist unzweifelhaft, dass (diese Eigenschaft der Elemente m1 der Menge M1) auf jedem (Element bzw. Objekt der Menge M2) in Übereinstimmung mit der Beschaffenheit (der Elemente bzw. Objekte der Menge M2) vorhanden ist“.
Tibetische Beispiele zu phyogs-chos:
a) M2 ist die Menge, die von den als „Laut“ (sgra) bezeichneten Objekten gebildet wird. M1 ist die Menge aller Objekte, die durch die charakteristische Eigenschaft „Gegenstände der visuellen Wahrnehmung zu sein“ (mig-shes kyi bzung-bya yin-pa) gebildet wird. Damit gehört kein Element von M2 zu M1, da die Elemente m2 (Laute) eben „nicht Gegenstände der visuellen Wahrnehmung sind“ (mig-shes kyi bzung-bya ma-yin-pa). Also gilt: M1 ⊅ M2. M1 ist nicht Obermenge von M2.

|
Abbildung 6 |
b) M2 ist die Menge aller Bäume (ljon-shing). M1 ist die Menge der „Objekte, die in der Nacht ruhen, und dabei die Blätter einrollen“ (mtshan-mo lo-ma ´khums te nyal-ba). Zwar gibt es Bäume, die nachts die Blätter einrollen, aber nicht alle Bäume (phyogs) haben diese Eigenschaft (ljon-shing mtha´-dag yod-pa ma yin-pa). Insofern haben nicht alle Bäume die konstitutive Eigenschaft von M1. Also gilt: M1 ⊅ M2. M1 ist nicht Obermenge von M2.
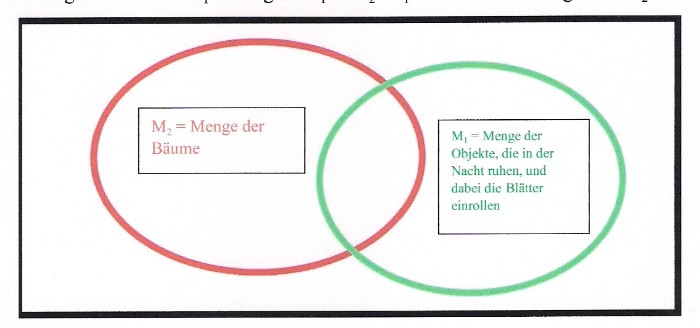 |
Abbildung 7 |
c) Es kann mehrere verschiedene Obermengen M1 geben, für die die Untermenge M2 die Bedingung phyogs-chos erfüllt. Ist M2 die Menge, die von den als „Laut“ (sgra) bezeichneten Objekten gebildet wird, so ist M1 als „die Menge dessen, was zu hören ist (mnyan-bya)“, zweifellos Obermenge von M2, denn die Eigenschaft „hörbar“ ist bei allen Lauten gegeben. Allerdings ist M2 auch Teilmenge der Obermenge M „Erkenntnisobjekte“ (gzhal-bya). Letzteres besagt, dass phyogs-chos als Gruppen bzw. - korrekter formuliert - als Mengen bildende Eigenschaft nicht im ontologischen Sinne etwas ist, was für „Laut“ (sgra) als solchen gleichsam wesentlich ist, bzw. das nur allen „Lauten“ zugeordnet werden kann. Denn als „Erkenntnisobjekte“ (gzhal-bya) lassen sich auch die Gegenstände der visuellen Wahrnehmung (mig-shes kyi bzung-bya) einordnen.
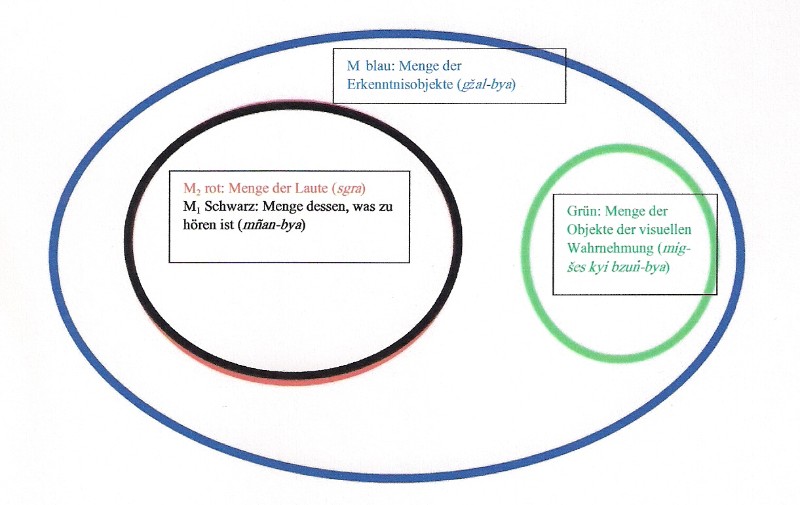 |
Abbildung 8 |
Betrachten wir nun die in der Formulierung von Cantor vorliegende Menge M1 in ihrem Verhältnis zur Menge M, so ist nun gefordert, dass M1 Untermenge bzw. Teilmenge der nun als Obermenge zu bezeichnenden Menge M ist (M1 ⊂ M).
M1 ist nur dann Teilmenge von M, wenn die Elemente m1 von M1 ausschließlich auch Elemente von M sind, also ohne Ausnahme zu M gehören (mthun-phyogs la kho-na yod-pa). Diese notwendige Voraussetzung für die Teilmengeneigenschaft wird in der tibetischen Logik als rjes-khyab bezeichnet. Dies bedeutet, dass alle Elemente der Menge M1 zu den Objekten gehören, die die Eigenschaft haben müssen, durch die die Menge M (mthun-phyogs) definiert ist.
Tibetische Beispiele zu rjes-khyab:
a) M1 bestimmt sich durch die Eigenschaft „hergestellt sein“ (byas-pa), umfasst also alle Objekte, die hergestellt sind (byas-pa). M bestimmt sich durch die Eigenschaft „beständig“ (rtag-pa), umfasst also alles, was „beständig ist“. Nun befindet sich in der Menge der Objekte (mthun-phyogs), die „beständig“ sind, etwas, was die Eigenschaft „hergestellt“ hat, überhaupt nicht (med-pa). Insofern gilt M1 ⊄ M. Tatsächlich sind die Elemente von M1 ausschließlich in der Komplementärmenge MC (mi-mthun-phyogs) von M vorhanden. M1 ist nicht Untermenge von M. Die rjes-khyab genannte Bedingung für M1 ⊂ M ist nicht erfüllt.
b) M1 sei bestimmt durch die Eigenschaft „Erkenntnisobjekt sein“ (gžal-bya). M sei bestimmt sich durch die Eigenschaft „unbeständig“ (mi-rtag-pa). Insofern sowohl Elemente von M (mthun-phyogs) als auch Elemente der Komplementärmenge MC (mi-mthun-phyogs) zu den Erkenntnisobjekten gehören, gilt in diesem Fall M1 ⊄ M. M1 ist nicht Untermenge von M. Die rjes-khyab genannte Bedingung für M1 ⊂ M ist nicht erfüllt.
c) M1 darf eine echte Untermenge von M sein. Es kann also Elemente von M geben, die nicht Elemente von M1 sind. Definiert man M1 als Menge aller Objekte, die „künstlich hergestellt“ (rtsol-byung) sind, und M als Menge von Elementen mit der Eigenschaft „unbeständig“ (mi-rtag-pa), so gehören nicht nur die die Elemente von M1 allein zur Menge mit der Eigenschaft „unbeständig“ (mi-rtag-pa la yod-pa kho na ma-yin-pa), denn die Eigenschaft „künstlich hergestellt zu sein“ ist nicht bei allen Elementen von M vorhanden (de de mtha´-dag la yod-pa ma yin-pa). So sind „Felsenberge“ (brag-ri) zwar nicht künstlich hergestellt, gehören aber zur Menge M der unbeständigen Objekte.
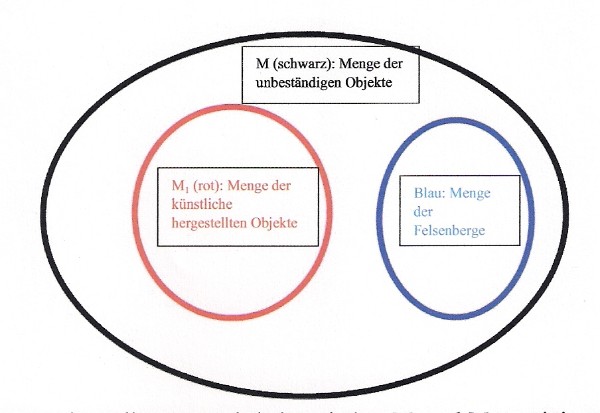 |
Abbildung 9 |
d) Letztendlich muss das Teilmengenverhältnis zwischen M1 und M unstrittig evident sein. Letzteres ist z. B. nicht der Fall, wenn M1 aus „Menschen besteht, die reden können“ (ngag-smra´i skyes-po pha-rol-po) und M die Menge der „Allwissenden“ (kun-mkhyen) ist. Damit taucht eine Parallele zu dem eingangs eigentlich mehr scherzhaft gemeinten Beispiel von der Allwissenheit deutscher Bundeskanzler sogar in der tibetischen Literatur auf.
Die Aussage M1 ⊂ M ist Äquivalent mit der Feststellung, dass es kein Element in der Untermenge bzw. Teilmenge M1 gibt, welches „außerhalb“ der Obermenge M, also in der Komplementärmenge von M (mi-mthun-phyogs), d.i. MC, liegt. Die tibetische Formulierung hierzu ist mi-mthun-phyogs la med-pa „ist nicht in der Komplementärmenge vorhanden“. Dieses wird in der tibetischen Logik als ldog-khyab bezeichnet.
Fassen wir diese beiden mit rjes-khyab und ldog-khyab beschriebenen, an sich simplen Aussagen noch einmal anhand einer Darstellung zusammen:
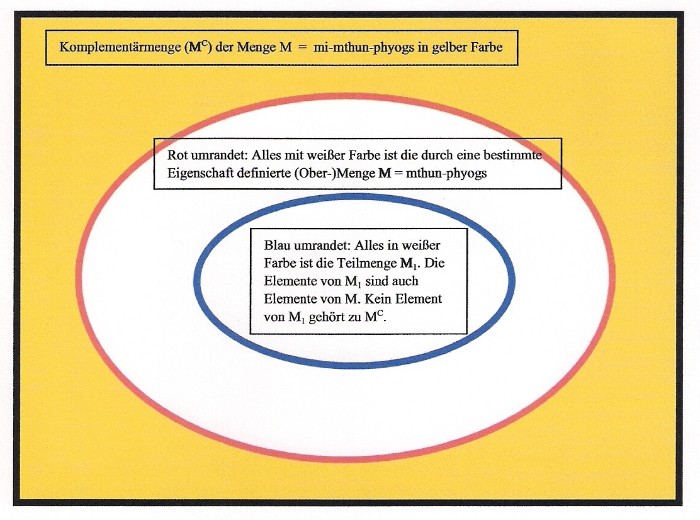 |
Abbildung 10 |
Die vorstehend skizzierten drei Bedingungen, nämlich
1. (für M2) „unstreitig die Eigenschaft aufzuweisen, die für die Bildung der Obermenge (M1) konstitutiv ist“ phyogs-chos,
2. (für M1) „ausschließlich zur Obermenge (M) (mthun-phyogs) gehören“ rjes-khyab
und
3. (für M1) „kein Element gehört zur Komplementärmenge (MC) (mi-mthun-phyogs)“ ldog-khyab,
dienen der Verifizierung der Aussagen M2 ⊂ M1 und M1 ⊂ M und werden im Tibetischen als tshul-gsum bezeichnet. Sie sind letztendlich nicht mehr als Kriterien für die Untersuchung konkret vorgelegter Mengen auf ihre Mengenrelation. Diese Untersuchungen verfolgen letztendlich nur das Ziel, die Aussage M2 ⊂ M zu verifizieren.
5. Die logische Aussageformel
Die tibetische Logik beschäftigt sich mit zweigliedrigen logischen Aussagen und der Formulierung von Kriterien, nach denen solche Aussagen als wahr oder falsch zu bewerten sind. Beispiele solcher Aussagen sind:
A.
1. sgra mi-rtag-pa
2. byas-pa´i phyir
1. Laut: (ist) unbeständig [~ etwas, was unbeständig ist].
2. Weil (Laut) hergestellt [~ etwas, was hergestellt ist] (ist).
B.
1. chos-dung dkar-po´i kha-dog chos-can dmar-po yin-par thal
2. kha-dog yin pa´i phyir
1. („Eigenschaftsträger“) Die Farbe des weißen Muschelhorns: (sie) ist rot, ist anzunehmen.
2. Weil (sie) Farbe ist.
C.
1. chos-dung dkar-po´i kha-dog chos-can chos-dung dkar-po´i kha-dog yin-par thal
2. chos-dung dkar-po´i kha-dog dang gcig yin-pa´i phyir
1. („Eigenschaftsträger“) Die Farbe des weißen Muschelhorns: (sie) ist die Farbe des weißen Muschelhorns, ist anzunehmen.
2. Weil (sie) dasselbe ist wie die Farbe des weißen Muschelhorns.
D.
1. de chos-can mi-rtag ste
2. ri-bong rva yin-pa´i phyir
1. („Eigenschaftsträger“) Jenes: (es) ist unbeständig.
2. Weil (jenes) das Horn eines Hasen ist.
Bei der strukturellen Analyse solcher Aussagen werden in den tibetischen Texten drei Begriffe verwendet, nämlich chos-can, chos und rtags. Zur Erklärung dieser Termini orientieren wir uns zunächst daran, dass die Aussagen in den Beispielen A – D strukturell gleich sind und die Form
X ist Y
Weil (X ist) Z
aufweisen. Die Tendenz, dass die Aussagen A – D eigentlich formelhaft gemeint sind, zeigt sich auch an der Verwendung des Demonstrativpronomens de „jenes“ im Beispiel D. Bleiben wir hier beim Beispiel A, so sind die Termini chos-can, chos und rtags wie folgt zuzuordnen:
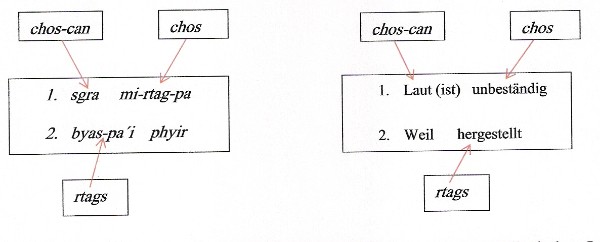 |
Abbildung 11 |
Fragen wir nun unter Orientierung an dieser Struktur, wie die tibetische Logik den Begriff rtags definiert, so wundert es nicht, wenn man folgende gängige Definitionen findet:
rtags su bkod-pa rtags kyi mtshan-nyid „Definition von rtags: Das, was man als rtags platziert.“
de sgrub kyi rtags su bkod-pa de sgrub kyi rtags kyi mtshan-nyid „Definition von rtags für die Verifikation von jenem: Das, was man für die Verifikation von jenem als rtags platziert“.
Angemerkt sei, dass ich hier mit Verifikationen die „Bewertung mit wahr oder falsch“ verstehe.
sgra mi-rtag-par sgrub-pa´i rtags su bkod-pa sgra mi-rtags-pa sgrub-pa´i rtags kyi mtshan-nyid „Definition von rtags für die Verifikation (der Aussage) „Laut (ist) unbeständig“: Das, was man für die Verifikation von „Laut (ist) unbeständig“ als rtags platziert.“
Verständlicher wird dies vielleicht für den westlichen Leser, wenn man unter Bezug auf die Formel
X ist Y
Weil (X ist) Z
wie folgt formuliert: rtags ist das, was man (in der vorstehenden Aussage) in die Stelle von Z einfügt. Dass die in der tibetischen Logik behandelte Aussage eine strukturierte Folge von Wörtern mit klar definierten Leerstellen ist, ergibt sich nicht nur aus dieser Definition. Der formelhafte Charakter zeigt sich auch an einer Bemerkung, die sich regelmäßig an die obige Definition anschließt: yod-med gang-rung yin na de sgrub kyi rtags yin-pas khyab. Dies besagt, dass man in die Leerstelle rtags (=Z) alles Beliebige einsetzen kann, und zwar unabhängig davon, ob es existiert oder nicht. Als Beispiel wird regelmäßig ri-bong rva „Horn eines Hasen“ aufgeführt und damit etwas genannt, was es nicht gibt. Man vergleiche hierzu auch das obige Beispiel D.
Auch wenn es den Einen oder Anderen langweilen mag, möchte ich doch zur weiteren Erklärung ein analoges Beispiel aus der Mathematik anführen. Nehmen wir die Formel
a:b=c,
so wird b Divisor genannt. Analog zur tibetischen Definition von rtags wäre Divisor somit als das zu definieren, was in der Formel a:b=c als b platziert wird. Konsens besteht hier in der Mathematik darüber, dass b eine Leerstelle für mögliche Zahlen ist. In der Aussage der tibetischen Logik besteht offenbar Konsens darüber, dass rtags eine Leerstelle für sprachliche formulierbare Eigenschaften spezifizierbarer Objekte der Anschauung oder der geistigen Vorstellung bzw. des Denkens ist, und zwar unabhängig davon, ob diese Objekte existieren oder nicht.
Die obige Formulierung yod-med gang-rung yin na de sgrub kyi rtags yin-pas khyab kann wie folgt übersetzt werden: „Alles, was existiert oder nicht existiert, wird von dem, was als rtags zur Verifikation jener (Aussage) eingesetzt werden kann, umfasst bzw. impliziert.“ Dies formuliert direkt, dass alles, was als rtags in die logischen Satzformeln eingesetzt werden kann, eine Obermenge zu der Menge dessen bildet, was existiert oder nicht existiert. Die Mengenrelation von Obermenge zur Untermenge sei hier unter Bezugnahme auf den tibetischen Ausdruck khyab mit dem Terminus „Implikation“ wiedergegeben.
Wenden wir uns nun dem Begriff chos zu, so finden wir hierzu folgende Definition:
bsgrub-bya chos su bzung-bar bya-ba bsgrub-bya´i chos kyi mtshan-nyid “Definition von zu verifizierendem chos: Das was als zu verifizierendes chos zu nehmen ist.“
Analog zu rtags wird also chos ebenfalls als Leerstelle der oben beschriebenen Aussageformel definiert und so überrascht es nicht, wenn man zusätzlich folgende Formulierung findet:
bdag-med yin na de sgrub kyi bsgrub-bya´i chos yin-pas khyab ste „wenn es ein nicht Existierendes ist, so wird dies von dem, was als zu verifizierendes chos für die Verifikation von jenem genommen wird, impliziert.“
Als Beispiel wird hier wiederum ri-bong rva „Horn eines Hasen“ aufgeführt und es folgt der Hinweis, dass das, was man in die Leerstelle chos der logischen Aussageformel einsetzen kann, größer ist, als die Menge dessen, was man gemeinhin mit chos als „Eigenschaft“ versteht:
des na bsgrub-bya´i chos yin na chos yin-pas ma khyab te „Wenn dem so ist, so wird das, was man als zu verifizierendes chos zusammenfasst, nicht von dem impliziert, was Eigenschaften sind.“
Anders gesprochen ist hiernach die Menge der Elemente, die man als chos in die entsprechende Leerstelle Y der logischen Aussagenformel
X ist Y
Weil (X ist) Z
einsetzen kann, eine echte Obermenge zur Menge aller „Eigenschaften“.
Wenden wir uns nun dem Begriff chos-can zu, so ist mir bisher eine mit den Begriffen chos und rtags vergleichbare Definition in den tibetischen Texten nicht begegnet. Betrachten wir aber Beispiele, wie
de chos-can ri-bong rva yin te
de yin-pa´i phyir
“Jenes (als) chos-can: es ist das Horn eines Hasen,
Weil es jenes ist“
oder
ri-bong gi rva chos can yod de
rva yin-pa´i phyir
“Das Horn eines Hasen: es ist vorhanden (~ es ist etwas, was existiert),
Weil es ein Horn ist.“
zeigen aber zweifelsfrei, dass chos-can ebenfalls als Leerstelle unserer oben erläuterten logischen Aussage
X ist Y
Weil (X ist) Z
verstanden wird.
Um die Struktur der logischen Aussage noch einmal zu verdeutlichen, sei zu dem Beispiel
sgra mi-rtag-pa
„Laut (ist) unbeständig [~ etwas, was unbeständig ist]“
festgestellt, dass sgra (Laut) nicht als grammatisches Subjekt und mi-rtag-pa „unbeständig [~ etwas, was unbeständig ist]“ nicht als grammatisches Prädikat zu bewerten ist. Dasselbe gilt z. B. für M1 und M, wenn wir die Formel M1 ⊂ M formulieren!
Beschäftigen wir uns noch einmal mit der logischen Aussage
1. sgra mi-rtag-pa
2. byas-pa´i phyir
1. Laut: (ist) unbeständig [~ etwas, was unbeständig ist]
2. Weil (Laut) hergestellt [~ etwas, was hergestellt ist] ist
so ist zunächst klar zu machen, dass das, was hier als chos-can eingesetzt ist, also sgra („Laut“), abstrakt gesprochen, extensional gemeint ist. Dies bedeutet, dass mit „Laut“ die Gesamtheit der Dinge gemeint ist, die man mit dem Begriff Laut zusammenfasst, also „alle Laute“. Die Verwandtschaft bzw. strukturelle Vergleichbarkeit mit dem Cantorschen Mengenbegriff wird dabei mehr als deutlich.
An der Stelle von rtags dieser Aussage finden wir byas-pa, das entweder als Adjektiv „hergestellt“ oder als Nomen „Etwas, was hergestellt ist“, „Hergestelltes“, zu interpretieren ist. Allerdings erscheint mir diese Unterscheidung für die Behandlung der Struktur der tibetischen Schlussfolgerung als unerheblich. Die Frage ist nämlich, ob die damit angesprochenen sprachlich unterschiedenen Zuordnungen von chos-can und rtags, also „(Laut ist) hergestellt“ und „(Laut ist etwas) Hergestelltes“, für die Relationen der hier zu behandelnden logischen Aussageformel überhaupt relevant sind.
6. Elemente der logischen Aussageformel und Mengen
Lösen wir uns von der umgangssprachlichen Formulierung, so geht es bei der Bewertung der tibetischen logischen Aussageformel nach wahr oder falsch um drei Relationen:
a) CHOS-CAN ← CHOS
b) CHOS-CAN ← RTAGS
c) RTAGS ← CHOS
Ich habe die Pfeile, die die Relationen zwischen den drei Hauptbestandteilen der tibetischen logischen Aussageformel darstellen, zunächst mit unterschiedlicher Farbe dargestellt, um offen zu lassen, ob es sich hier um verschiedene Relationen handelt. Betrachten wir zunächst die Relation b) (CHOS-CAN ← RTAGS) anhand des vorstehenden Beispiels sgra mi-rtag-pa, byas-pa´i phyir. Die Bedingungen, die hier an CHOS-CAN gestellt werden, um die Aussage als wahr bewerten zu können, werden z. B. wie folgt formuliert:
1. rtsod-gzhir bzung-ba „Gegenstand eines Streites sein“. CHOS-CAN als Leerstelle markiert insofern den Gegenstand einer Diskussion oder einer In-Frage-Stellung.
2. khyod byas-par tshad-mas nges-pa „es ist durch wahre Erkenntnis gewiss, das du hergestellt (byas-pa) bist“. Jedwede Interpretation dieses Satzes dürfte hier zwischen „du bist hergestellt“ oder „du bist hier etwas, das ein Hergestelltes ist“, nicht unterscheiden können, so dass das hier auftauchende, ansonsten in die Leerstelle RTAGS eingesetzte byas-pa, auch extensional gemeint ist, also alles was hergestellt ist bzw. alles, was die Eigenschaft hergestellt besitzt oder alles Hergestellte impliziert.
Die Bezeichnung für etwas, was in die entsprechenden Leerstelle CHOS-CAN der logischen Aussageformel eingesetzt ist und das diese Bedingungen erfüllt, ist shes-´dod chos-can skyon-med „fehlerfreies CHOS-CAN“, über das man etwas zu wissen wünscht.“
Um die logische Aussagenformel als wahr zu bewerten, muss die Relation CHOS-CAN ← RTAGS unter anderem eine Bedingung erfüllen, die als phyogs-chos bezeichnet wird. Für diesen Begriff habe ich oben die Übersetzung „eine den Elementen einer Menge (phyogs) gemeinsame Eigenschaft (chos)“ vorgeschlagen. Die oben anhand von tibetischen Beispielen gegebenen Erläuterungen zeigen, dass phyogs hier eine Menge bezeichnet, die über das in CHOS-CAN Eingesetzte (z.B. sgra) definiert ist.
Betrachten wir nun die Leerstelle RTAGS. Auch wenn wir hierfür das Eingesetzte sprachlich adjektivisch interpretieren, ist es in jedem Fall auch extensional gemeint. Die hier möglichen Formulierungen, nämlich
dass
jedes Elemente der mit sgra („alle Laute“) gegebenen Menge (phyogs) in der Leerstelle CHOS-CAN
die in der Leerstelle RTAGS eingesetzte Eigenschaft byas-pa „hergestellt“
hat, oder
dass
alle sgra („Laute“)
auch die Eigenschaft (chos) der Menge haben, die durch die Eigenschaft byas-pa „hergestellt sein“ konstituiert wird,
bedeuten beide meiner Meinung nach dasselbe, nämlich
dass die in
CHOS-CAN eingesetzte Menge
eine Teilmenge der durch RTAGS definierten Menge ist.
Die Grundbedingung dieser Analyse ist, dass alles, was in der Leerstelle CHOS-CAN eingesetzt werden kann, immer extensional gemeint ist. Dagegen spricht auch nicht ein Beispiel aus logischen Aussageformeln wie das Folgende:
byas pa chos-can, sgra mi rtag-par sgrub-pa´i rtags yang-dag yin[3] „Hergestellt sein“ ist ein korrektes rtags für den logischen Schluss, dass ‚Laut unbeständig ist‘.“
Natürlich ist die Eigenschaft „Hergestellt sein“ wohlunterscheidbares Objekt unseres Denkens. Die Eigenschaft „Hergestellt sein“ kann auch zu Mengen oder Obermengen gehören, entweder als Element oder als Teilmenge, die nur aus einem Element, nämlich der Eigenschaft „Hergestellt sein“ besteht. So wird durch die Leerstelle RTAGS in der logischen Satzformel die Menge aller Objekte gebildet, die in diese Leestelle eingesetzt werden können. Bezeichnen wir diese Elemente als rtags, so bilden die Elemente, die die Eigenschaft „Korrektes rtags sein“ haben, natürlich eine Teilmenge, die man als {rtags yang-dag} bezeichnen kann. Natürlich gilt dann auch z. B. {byas-pa} ⊂ {rtags yang-dag} oder byas-pa ∈ {rtags yang-dag}. Dieses und nur dieses sagt der oben aus dem Buch von Tom Tillemans zitierte Satz aus.[4]
Wir können deshalb die Bedingung für die Relation CHOS-CAN ← RTAGS, die für die Bewertung einer logischen Aussage als wahr bestehen muss, als CHOS-CAN ⊂ RTAGS formulieren bzw. interpretieren.
Betrachten wir nun die Relation RTAGS ← CHOS, so definiert das in der Leerstelle CHOS eingesetzte, z. B. mi-rtag-pa („unbeständig“), wiederum, wie schon oben ausführlich erläutert, eine Menge (mthun-phyogs), also z. B. „alles, was Unbeständiges ist“, und deren Komplementärmenge (mi-mthun-phyogs). Bedingung für die Bewertung der logischen Aussage als wahr ist, dass die Elemente der Menge, die durch das in RTAGS Eingesetzte definiert wird, also z. B. „alles, was Hergestelltes ist“, zu der mthun-phyogs gehören, was wir als RTAGS ⊂ CHOS
formulieren. Diese Bedingung wird als rjes-khyab bezeichnet.
Diese Bedingung impliziert des Weiteren, dass kein Element der Menge, die durch das in RTAGS Eingesetzte (z. B. byas-pa) definiert wird, in der zugehörigen Komplementärmenge (mi-mthun-phyogs) von CHOS vorkommt. Dies wird als ldog-khyab bezeichnet.
Aus CHOS-CAN ⊂ RTAGS und RTAGS ⊂ CHOS resultiert, dass CHOS-CAN ⊂ CHOS als wahr zu bewerten ist. Die tibetische Bezeichnung für die Teilmenge dessen, was in der Leerstelle RTAGS eingesetzt wird, und bei der die Bedingungen CHOS-CAN ⊂ RTAGS und RTAGS ⊂ CHOS erfüllt werden, ist rtags yang-dag.
7. Schlussbemerkung
Um an dieser Stelle einem möglichen Irrtum vorzubeugen, möchte ich ausdrücklich betonen, dass ich nicht die Ansicht vertrete, die tibetischen Gelehrten hätten vor Cantor Grundbegriffe der elementaren Mengenlehre erfunden und verwendet. Im Zusammenhang mit mathematischen Kenntnissen der Tibeter habe ich über lineare Gleichungen im Zusammenhang mit den Berechnungen der Positionen der Planeten und der Mittelpunktsgleichung des Mondes gesprochen. Dies bedeutet nicht, dass die Tibeter die lineare Algebra kannten. Vielmehr sind die entsprechenden umständlichen Rechenmethoden der tibetischen Astronomie heute nur vor dem entsprechenden Hintergrund algebraischer Kenntnisse verständlich zu erklären. Das Gleiche gilt für die tibetische Logik. Positiv formuliert ist sie eine Art Vorläufer von Teilen der elementaren Mengenlehre. Vergleichbares gilt für die als bsdus-grva bezeichnete Disziplin, die auf der Basis von Definitionen unterschiedlicher Phänomene und Begriffe, also von Mengen von Objekten der Anschauung und des Denkens, und deren konstitutiven Eigenschaften, die innere Ordnung dieser Phänomene anhand des extensiven Gebrauchs der obigen logischen Aussageformel einübt. Vielleicht könnte man auch formulieren, dass diese Disziplin dazu dienen soll, anhand der logischen Aussageformel die Unordnung in den Köpfen von Menschen über die Ordnung der Phänomene zu beseitigen. Insofern ist bsdus-grva auch eine Art Mengenlehre über die Ordnung der Phänomene und Begriffe.
[1]Georg Cantor:
Beiträge zur Begründung der transfiniten Mengenlehre. In: Mathematische Annalen 46 (1895), S. 481.
[2] Quelle: Wikipedia Datei: Veranschaulichung einer Menge.svg
[3] Tom J. F. Tillemans: Scripture, Logic, Language. Essays on Dharmakirti and his Tibetan Successors. Boston 1999, S. 143.
[ 4] Ich möchte an dieser Stelle diese Einführung nicht mit zunächst kompliziert erscheinenden, weiteren vergleichbaren Beispielen aus
bsDus-grva-Texten überfrachten. So lassen sich die folgenden beiden logischen Aussagen, die ich aus dem in den Anmerkungen 22 und 24 aufgeführten Texten einfach nur kopiert habe, ebenso einfach analysieren und interpretieren, wie das vorstehend aus dem Buch von Tillemans zitierte Beispiel:
KHYOD KHYOD KYI RTAGS KYIS SGRA MI-RTAG -PAR SGRUB-PAR BYED-PA'I SHES -'DOD CHOS-CAN SKYON-MED KYI STENG DU 'GOD-TSHUL DANG MTHUN-PAR YOD-PA NYID DU TSHAD-MAS NGES-PA'I PHYIR
KHYOD KHYOD KYI RTAGS KYIS SGRA MI-RTAG-PAR SGRUB-PAR BYED-PA'I MTHUN-PHYOGS KHO-NA LA YOD-PA NYID DU TSHAD-MAS NGES-PA'I PHYIR
Im Übrigen lag die Schwierigkeit solcher tibetischer Satzbandwürmer für meine früheren Studenten darin, dass bei nicht hinreichender Kenntnis der tibetischen Schriftsprache mit dem Wörterbuch in der rechten und irgendeiner grammatischen Beschreibung des Tibetischen in der linken Hand solchen Texten nicht beizukommen war, zumal die zur Verfügung stehenden bzw. gebräuchlichen Bedeutungsansätze einzelner Termini für diese technische Literatur selbst bei sogenannten korrekten wörtlichen Übersetzungen zu völlig unverständlichen Satzgebilden in der Zielsprache führten. Die zugängliche Literatur über tibetische Logik ist voll von unverständlichen Sätzen der folgenden Art:
„(1) it is an indefinite sign in the proof of that and (2) it is a common locus of (a) not being ascertained as existent in the similar class in the proof of that by a person for whom it has become the property of the subject in the proof of that, and (b) that person does not ascertain it as existing in the dissimilar class in the proof of that.” (Katherine Manchester Ro-gers: Tibetan Logic. New York 2009, S. 339)





