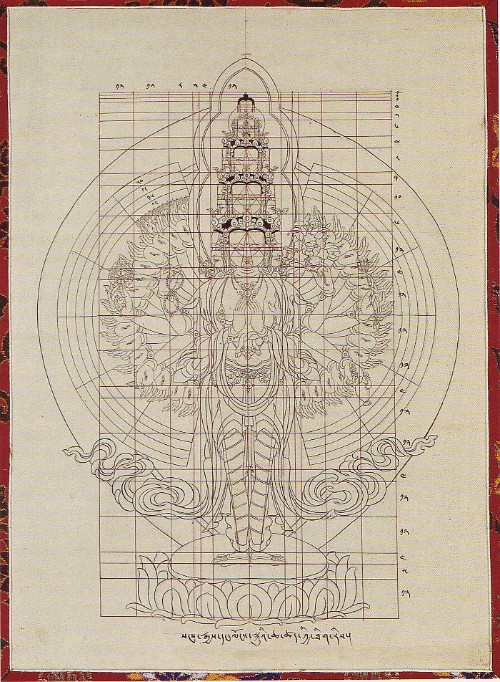
Tibetische Geometrie

Mit tibetischer Geometrie wird die Gesamtheit des Wissens im historischen Tibet bezeichnet, das für die Konstruktion von geometrischen Figuren wie Rechtecken, Quadraten, Dreiecken, Hexagrammen, Kreisen usw. und im Hinblick auf die Winkelteilung angewendet wurde. Solche Kenntnisse der Geometrie waren erforderlich für die auf Abbildung 1 ersichtliche Basis-Konstruktion von Figuren in der tibetischen Thangka-Malerei bzw. in der Bildhauerei. Das geometrische Wissen der Tibeter ist noch weitgehend unerforscht. Angesichts der rasant fortschreitenden Veränderungen im heutigen Tibet besteht die Gefahr, dass dieses Wissen über die geometrischen Techniken der einstmals führenden Malschulen des alten Tibet verloren geht bzw. von Techniken der modernen Mathematik überlagert wird.

Die einzigen Forscher, die Material für die mathematische Beurteilung der Konstruktionstechniken der Thangka-Malerei veröffentlicht haben, waren David und Janice Jackson. Leider war deren Interesse an der Geometrie offenbar nicht sehr groß, so dass eine systematische Erforschung des geometrischen Wissens der Thangka-Maler, mit denen die beiden zusammenarbeiteten, unterblieben ist. Zur tibetischen Ikonometrie gibt es zahlreiche tibetische Literaturwerke. Ob diese Werke über die Lehre von den Proportionen tibetischer Heiligen- oder Götterfiguren hinausgehend auch geometrische Verfahren beschreiben, ist unbekannt.

Inhaltsverzeichnis:

1. Zeichengeräte
2. Konstruktion von Rechtecken
3. Winkelteilung und Konstruktion von Orthogonalen
4. Dreiteilung von rechten Winkel und Hexagramme
5. Literatur

1. Zeichengeräte

David und Janice Jackson verweisen in ihrem 1984 veröffentlichenten Buch „Tibetan Thangka Painting“ auf den Gebrauch von Zirkeln (Abbildung 2) zur Konstruktion von Kreisen. Aus Jacksons Buch entnehmen wir auch, dass es zwei unterschiedliche Arten von Zirkeln gab. Zur Zeichnung kleiner Kreise benutzte man das auf der Abbdildung 2 abgebildete Instrument. Die tibetische Bezeichnung für diese Art von Zirkel wird mit skor-thig angegeben. Dieser Zirkel besteht aus zwei flachen, hölzernen Stäben, die jeweils an einem Ende gelenkig verbunden sind. Einer der Stäbe hat an seinem anderen Ende eine Spitze aus Metall, die zur Fixierung des Zirkels auf der Unterlage dient und den Mittelpunkt des Kreises markiert. Am Ende des zweiten, beweglichen Stabes ist als Vorrichtung, mit der der Kreis oder Kreisabschnitt auf der Unterlage gezeichnet wird, ein Stück angespitzter Holzkohle angebracht.

Für große Kreise wurde der zweite, der rechts abgebildete Stangenzirkel verwendet, der skor-pang genannt wurde. Bei ihm können Kreismittelpunkt und Radius an einer Holzstange parallel verschoben werden.

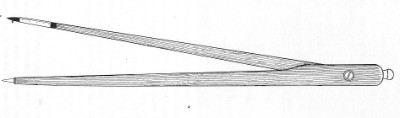Abbildung 2: Aus Holz gefertigter tibetischer Zirkel (skor-thig)		Abbildung 3: Tibetischer Stangenzirkel (skor-pang)		Abbildung 4: Ein tibetischer Künstler arbeitet mit dem Zirkel

Zur Zeichnung einer geraden Linie verwendeten die tibetischen Maler nicht ein Lineal, sondern einen vorher durch einen Farbbeutel (thig-rkyal) gezogenen Faden (thig-rkud), der über die Grundfläche gespannt wird und durch den Zeigefinger so in eine ruckartige Bewegung versetzt wird, dass sich eine Gerade auf der Grundfläche abbildet. Die Methode wird durch das rechte Bild (Abbildung 6) verdeutlicht, das ebenfalls von David und Janice Jackson stammt. Linien, die mit trockenem Pulver gezogen wurden, nannte man skam-thig. Daneben gab es mit einem feuchten Faden erzeugte Linien, die rlon-thig genannt wurden.

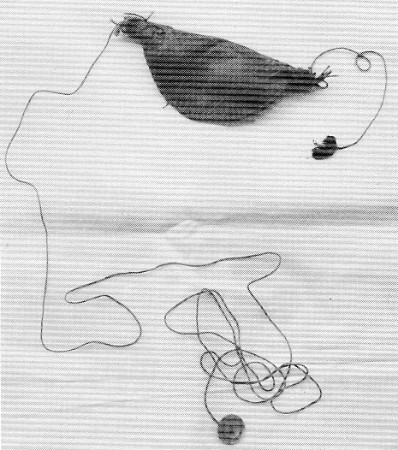Abbildung 5: Konstruktionsfaden mit Farbbeutel		Abbildung 6: Ein Künstler zeichnet eine gerade Linie mit dem Konstruktionsfaden

Zweifelsfrei ersetzt dieser Konstruktionsfaden zur Zeichnung einer Geraden vollwertig das schon von den Griechen (Euklid) verwendete Lineal ohne Einteilung von Maßeinheiten, zumal die auf den Zeichnungen (siehe Abbildung) eingetragenen Maßgrößen keine absolut festgelegten Maße waren. Vielmehr handelt es sich bei den Zahlenangaben um die Größe von Proportionalmaßen, die je nach Bildgröße unterschiedlich groß waren.

2. Konstruktion von Rechtecken

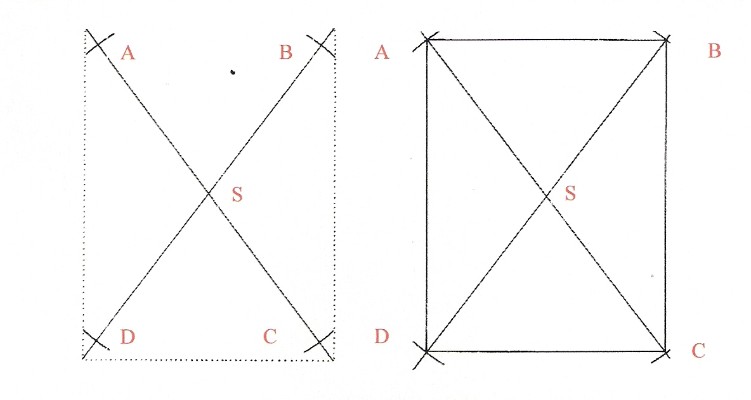
Mit diesen beiden „euklidischen Werkzeugen“ waren die Tibeter zunächst in der Lage, Rechtecke zu konstruieren. Hierzu zeichnete man mit dem Konstruktionsfaden zwei beliebige, sich schneidende Geraden, die zur-thig genannt wurden (Abbildung 7a). Um den Schnittpunkt S  schlägt am mit dem Zirkel einen Kreis, der die beiden Geraden in den Punkten A, B, C und D schneidet. Durch die Verbindung der Punkte A, B, C und D durch den Konstruktionsfaden erhält man ein Rechteck (Abbildung 7b).

Abbildungen 7a und 7b: Konstruktion eines Rechtecks		Abbildung 8: Halbierung eines Winkels und Errichtung einer Orthogonalen

 3. Winkelteilung und Errichtung von Orthogonalen

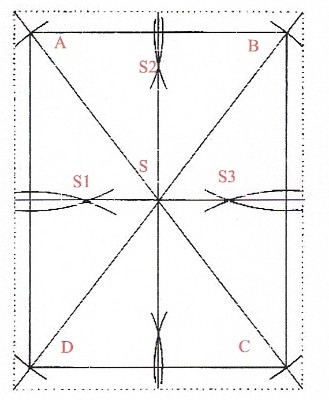
Aus der Abbildung 8 kann man, entnehmen, dass das Verfahren zur Teilung eines Winkels, zur Teilung eine Strecke sowie der Errichtung einer senkrechten Linie (Orthogonalen) auf einer vorgegebenen Strecke in Tibet ebenfalls bekannt war. Betrachtet man hierzu den Winkel A, S, D, so wurde, um diesen Winkel zu halbieren, jeweils ein Kreis jeweils um A und D mit gleich großem und hinreichend großem Radius geschlagen. Die Verbindungslinie des Schnittpunktes beider Kreise S1 mit S ergibt dann die Winkelhalbierende. Das Gleiche gilt für den Winkel A, S, B. Betrachten wir die Konstruktion von S1 so steht zweifelsfrei fest, dass die Tibeter sowohl das Problem der Errichtung einer Senkrechten auf einer Geraden wie auch das Problem der Halbierung einer Strecke mit den „euklidischen Werkzeugen“ lösen konnten. Dazu bedurfte es nur der Zeichnung des zweiten Schnittpunktes der beiden Kreise, die sich in S1 schneiden.
 
David und Janice Jackson weisen daraufhin, dass man zur Ermittlung der Schnittpunkte S1, S2 und S3 anstelle des Zirkels auch den Konstruktionsfaden verwendete, wobei man einen festen Punkt des Fadens an den Punkten A oder D fixierte und einen zweiten, festen Punkt des gespannten Fadens zum Einritzen der sich in S1 schneidenden Kreisbögen mit dem Daumennagel verwendete. Natürlich entspricht dies dem Gebrauch des Zirkels und man verlässt damit nicht den Bereich der euklidischen Werkzeuge.

4. Dreiteilung von rechten Winkeln und Hexagrammme

Bekanntlich kann man mit den euklidischen Werkzeugen einen beliebig großen Winkel nicht in drei gleich große Teile teilen. Dies gilt nicht für rechte Winkel. Im Hinblick auf die Teilung von Winkeln stellt sich somit die Frage, ob die Tibeter die Aufgabenstellung der Dreiteilung eines rechten Winkels lösen konnten. Hierzu begegnen einem in der tibetischen Astronomie Zeichnungen, in denen der Kreis (Abbildung 9) mit feinen roten geraden Linien in zwölf gleiche Sektoren geteilt ist. Diese stellen hier Sektoren auf der flachen Erdoberfläche dar, die sich um den in der Mitte befindlichen Weltberg gruppieren. Eine solche Kreisteilung setzt, so sie denn mit dem Zirkel und dem Konstruktionsfaden durchgeführt wurde, die Kenntnis der Dreiteilung eines rechten Winkels voraus.

Eine Lösung dieser Fragestellung nach der Dreiteilung eines rechten Winkels ergibt sich aus den Zeichnungen von Mandala und tibetischen Thankas, auf denen sich Konstruktionszeichnungen von Hexagrammen, auch „Sechsstern“ genannt, finden (Abbildung 10). Konstruiert wird ein solches Hexagramm mit zwei gleichseitigen Dreiecken. Die leicht durchzuführende Konstruktion von gleichseitigen Dreiecken war nach dem Vorstehenden den tibetischen Künstlern sicherlich bekannt. Die Verbindung (Abbildung 11) der Punkte A, B, C, D, E und F, von mir grün gestrichelt eingezeichnet, ergibt ein regelmäßiges Sechseck. Der Winkel A, B, S, von mir rot eingezeichnet, beträgt 60°. Da die Winkelteilung bekannt war, konnte man also Winkel von 30° konstruieren und damit die Zwölfteilung des Kreises durchführen, was der Dreiteilung von rechten Winkeln gleichkommt.

Es ist aber auch nicht auszuschließen, dass die leicht durchzuführende Konstruktion des regelmäßigen Sechseckes in Tibet die Grundlage für die Konstruktion des Hexagramms und der Teilung eines Kreises in 12 Sektoren bildete. Eine einfache, uns bekannte Methode dieser Konstruktion ist auf Abbildung 12 dargestellt.

Leider ist es offenbar so, dass diejenigen, die sich mit tibetischer Kunst beschäftigt haben, bisher für die hochentwickelten geometrischen Kenntnisse der verschiedenen großen Malschulen Tibets weniger Interesse gezeigt haben. So besteht heute die Gefahr, dass dieses Wissen eines Tages soweit verloren gegangen ist, dass es von uns nicht mehr rekonstruiert werden kann.

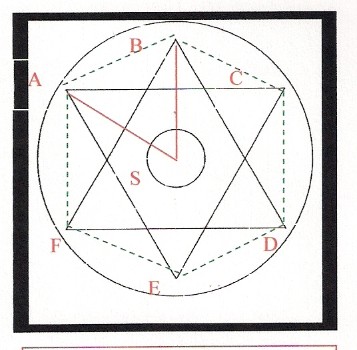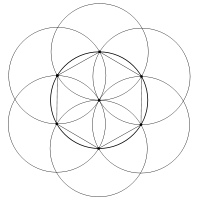Abbildung 9: Tibetischer astronomischer Thangka mit Teilung eines Kreises in zwölf gleich große Teile		Abbildung 10: Tibetischer Thangka mit einem regelmäßigen Sechseck (Hexagramm)		Abbildung 11: Zwei ineinandergeschachtelte, gleichseitge Dreiecke ergeben ein Hexamgram		Abbildung 12: Konstruktion eines regelmäßigen Sechsecks

5. Literatur

David P Jackson and Janice Jackson: Tibetan Thangka Painting. Methods & Materials. Second and Revised Edition. London 1988.
Loden Sherab Dagyab: Tibetan Religious Art. Part I-II. Wiesbaden 1977.
Henns, Michael: Vom rechtem Maß und richtiger Zahl. Die Ikonometrie in der buddhistischen Kunst Tibets. In: Tibet. Klöster öffnen ihre Schatzkammern. Kulturstiftung Ruhr, Essen und Hirmer Verlag München, 2006, S. 105-113.

Autor: Dieter Schuh, 2010. Bildnachweise: Abbildung 1 aus: Tibet. Klöster öffnen ihre Schatzkammern. Kulturstiftung Ruhr, Essen und Hirmer Verlag München, 2006, S. 91. Abbildungen 2-8 aus: David P Jackson and Janice Jackson: Tibetan Thangka Painting. Methods & Materials. Second and Revised Edition. London 1988.