Tibetischer Sandabakus (sa-gzhong)
Ein Tibetischer Sandabakus (sa-gzhong), auch Tibetisches Sandrechenbrett genannt, ist ein Rechenhilfsmittel zur Durchführung von Rechenaufgaben für Berechnungen zum tibetischen Kalender und zur tibetischen Astronomie. Er wurde ausschließlich für die tibetische Kalenderrechnung und die tibetische Astronomie verwendet. Sein Gebrauch hat, wie die seit dem 11. Jahrhundert in Tibet bekannte Astronomie des Kālacakratantra, indischen Ursprung. Seine Verwendung in Tibet ist wenigstens eintausend Jahre alt. Der Sandabakus wird bis in die Gegenwart von tibetischen Astronomen zur Berechnung des tibetischen Kalenders verwendet.
 | |  |
Der Astronom Pelgön Thrinle rechnet mit dem Sandabakus | | Der tibetische Regent und Astronom Sanggye Gyatsho mit einem Sandabakus |
Für Rechenaufgaben in anderen Bereichen, insbesondere in der Finanzverwaltung der tibetischen Regierung, wurde der tibetische Abakus mit losen Steinen benutzt.
Inhaltsverzeichnis
1. Das Rechengerät
2. Rechenanweisungen und Grundrechenarten
2.1. Platzieren bzw. Schreiben von Zahlen
2.2. Addieren mehrstelliger natürlicher Zahlen
2.3. Subtrahieren mehrstelliger natürlicher Zahlen
2.4. Multiplizieren mehrstelliger natürlicher Zahlen
2.5. Division mehrstelliger natürlicher Zahlen
3. Durchführung astronomischer Berechnungen
4. Rechnen mit Zahlen im Sexagesimalsystem
4.1. Addition und Subtraktion
4.2. Multiplikation und Umrechnung auf Stellenwerte
4.3. Division
5. Literatur
1. Das Rechengerät
Der tibetische Sandabakus war ein flaches Brett, dessen Rand mit einer schmalen Leiste versehen war, damit der Sand nicht vom Brett herunterfallen konnte. Ein Ende des Bretts war abgerundet, während das andere gerade abgeschnittene Ende eine Art Tasche aufwies, in der der Sand aufbewahrt wurde.
Vor dem Beginn der Rechnungen wurde der sehr feine Sand gleichmäßig auf dem Brett verteilt. Geschrieben wurde mit einem hölzernen, angespitzten Griffel, der sa thur genannt wurde. Die in den Sand geritzten Zahlen konnten leicht mit dem Daumen weggewischt und an ihre Stelle neue Zahlen geschrieben werden. Dies war wesentlich für die Durchführung der Rechenoperationen. Entsprechend wird „wegwischen“ (byi-pa; dbyi-ba, bsubs-pa, dor-ba) bei den Grundrechnungsarten als mathematische Rechenoperation aufgeführt. Geschrieben wurden die Zahlen in der nachfolgend dargestellten üblichen Form tibetischer Ziffern.
2. Rechenanweisungen und Grundrechenarten
Astronomische Berechnungen werden grundsätzlich nach einer Folge von Rechenanweisungen durchgeführt, die Computerprogrammen gleichen. Die wichtigsten Handlungsanweisungen dieser Programmiersprache sind neben dem schon erwähnten Tilgen bzw. Wegwischen von Zahlen (grangs) folgende:
1. Platzieren von natürlichen Zahlen auf bestimmten Stellen (gnas) des Sandabakus, was einem Vorgang des Niederschreibens ('dri-ba) von Zahlen gleichkommt. Hierbei ist der Stellenwert dieser Stellen stets ≠ 10. Stellen dieser Art sind grundsätzlich untereinander, also von oben nach unten, angeordnet.
2. Umrechnen (bsgril-ba) der den Stellenwert überschreitenden natürlichen Zahl auf einer Stelle auf die nächst größere Stelle. Dies ist immer dann erforderlich, wenn auf Grund einer mathematischen Operation (z. B. einer Multiplikation) die auf der jeweiligen Stelle notierte Zahl größer als der Stellenwert ist. Dieser Vorgang ist eigentlich nicht mehr als eine Division einer Zahl durch den Stellenwert und anschließender Addition des Ergebnisses (ohne Rest) zu der nächst höheren Stelle, während der Rest auf der vorgegebenen Stelle verbleibt.
3. Addieren (bsnan-pa) (von natürlichen Zahlen).
4. Subtrahieren ('phri-ba) (von natürlichen Zahlen).
5 .Multiplizieren (bsgyur-ba) (von natürlichen Zahlen).
6. Dividieren (bgo-ba) (von natürlichen Zahlen).
Tibetische Abhandlungen zur Astronomie behandeln diese Rechenoperationen, wenn überhaupt, nur sehr kurz. Ein Student der tibetischen Astronomie war deshalb darauf angewiesen, dass ein Lehrer ihm die Durchführung dieser Operationen durch mündliche Unterweisung übermittelte.
2.1. Platzieren bzw. Schreiben von Zahlen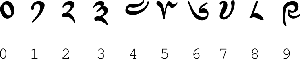
Zwar wurden Zahlen auf dem Sandabakus mit den rechts aufgeführten tibetischen Ziffern bzw. Zahlzeichen notiert, doch kommen in den Rechenanweisungen der tibetischen Astronomie weder diese Ziffern noch die entsprechenden tibetischen Zahlworte vor. Vielmehr werden sogenannte symbolische Zahlwörter verwendet.
Beispiele (hier jeweils nur eine Auswahl) für symbolische Zahlwörter:
Für die Zahl 0: Leere (stong-pa) oder Himmel (nam mkha').
Für die Zahl 1: Hase (ri-bong), Mond (zla-ba), Körper (gzugs) oder Rhinozeros (bse-ru).
Für die Zahl 2: Hände (lag), Auge (mig), Paar (zung) oder Gangart (der Sonne) (bgrod).
Für die Zahl 3: Welt ('jig-rten), Spitze (rtse-mo) oder Feuer (me).
Für die Zahl 4: Ozean (rgya-mtsho), Fluss (chu-bo), Teufel (bdud) oder Fuß (rkang).
Für die Zahl 5: Sinnesorgan (tib.: dbang po), Element (tib.: 'byung ba) oder Pfeil (tib.: mda')
Für die Zahl 6: Geschmack (ro), Jahreszeit (dus) oder Lebewesen ('gro-ba).
Für die Zahl 7: Kostbarkeit (rin-chen), Weiser (thub-pa) oder Planet (gza').
Für die Zahl 8: Gott (lha), Verlangen (sred-pa) oder Glück (bkra-shis).
Für die Zahl 9: Wurzel (rtsa), Schatz (gter) oder Loch (bu-ga).
Für die Zahl 10: Himmelsrichtung (phyogs), Kraft (stobs) oder Reichtum ('byor-ba).
usw., usw..
Dabei ist zu beachten, dass die so wiedergegebenen Zahlen stets von rechts nach links geschrieben wurden. Die in den tibetischen Rechenvorschriften aufgeführte Zahl
„Pfeil (5) Geschmack (6)“ ist also = 65,
die Zahl
„Wurzel (9) Jahreszeit (6) Auge (2) Planet (7) ist = 7269.
Die Rechenvorschrift "Multipliziere 65 mit 7269" erscheint in den tibetischen Rechenanweisungen entsprechend als
multipliziere "Pfeil Geschmack" mit "Wurzel Jahreszeit Auge Planet".
Ein tibetischer Astronom hatte zur Durchführung von Rechnungen auf dem Sandabakus zunächst zahlreiche symbolische Zahlwörter auswendig zu lernen und die besondere Schreibregel der Zahlen zu beachten.
2.2. Addieren mehrstelliger natürlicher Zahlen
Als Voraussetzung für die Addition mit dem Abakus hat der Astronom das Addieren von einstelligen Zahlen, wie z.B. 6 + 9, 2 + 3 usw., auswendig gelernt. Als Beispiel für die Durchführung der Addition mit dem Abakus sei von der Aufgabenstellung 11 + 68 + 89 ausgegangen. Hierzu schreibt man die drei Zahlen untereinander und geht nach dem folgenden Verfahren vor, wobei auf dem Abakus immer nur eine Spalte erscheint, die durch Wegwischen und Ergänzung von Zahlen verändert wird.
| (1.) Aufgabenstellung: 11, 68 und 89 sind zu addieren | (2.) 9 + 8 (wird getilgt) = 17 (wird notiert). | (3.) 7 + 1 (wird getilgt) = 8 (wird notiert). | (4.) 8 + 1 (wird getilgt) = 9 (wird notiert). | (5.) 9 + 6 (wird getilgt) = 15 (wird notiert). | (6.) 5 + 1 (wird getilgt) = 6 (wird notiert). |
|---|
| 11 | 11 | 18 | 18 | 118 | 168 |
| 68 | 67 | 6_ | 6_ | 5_ | |
| 89 | 8_ | 8_ | 9_ | | |
| | 1_ | 1_ | |
2.3. Subtrahieren mehrstelliger natürlicher Zahlen
Als Voraussetzung für die Subtraktion mit dem Abakus hat der Astronom das Subtrahieren von einstelligen Zahlen, wie z.B. 10 − 9, 4 − 2 usw., auswendig gelernt. Als Beispiel zur Durchführung der Subtraktion sei hier von der Aufgabenstellung 1111 − 707 ausgegangen. Minuend und Subtrahend werden untereinandergeschrieben.
| (1.) Aufgabenstellung: von 1111 ist 707 abzuziehen | (2.) 10 − 7= 3. Tilge 1 und 7. Notiere 3 (zu addieren) | (3.) Addiere 3 | (4.) 10 − 7= 3. Tilge 1 und 7. Notiere 0 und 3 (zu addieren) | (5.) Addiere 3 |
|---|
| 1111 | 111 | 411 | 401 | 404 |
| 707 | 307 | 7 | 3 |
2.4 Multiplizieren mehrstelliger natürlicher Zahlen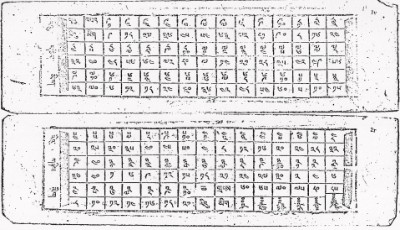
Als Voraussetzung für die Durchführung der Multiplikation mehrstelliger Zahlen hat der Astronom das kleine Einmaleins auswendig zu lernen. Die entsprechende Multiplikationstafel wird im Tibetischen „Neunerende“ (dgu -mtha') genannt, da solche Tafeln mit 9•1 beginnen und bei 2•10 aufhören.
Die nebenstehende Multiplikationstafel beginnt mit der Aufführung ihrer tibetischen Bezeichnung: dgu mtha ri'u mig „Tafel mit dem Neunerende“. In der ersten Zeile verzeichnet sie Multiplikator und Multiplikand, die übereinander geschrieben werden. Darunter, in der zweiten Reihe, wird das Ergebnis notiert.
Die Zahlen der ersten beiden Reihen der Multiplikationstafel:
1. Zeile (oben, Multiplikator) | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 8 | 8 | 8 |
|---|
| 1. Zeile (unten, Multiplikand) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 |
|---|
| 2. Zeile (Produkt) | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 8 | 16 | 24 |
|---|
Bei der Multiplikation von mehrstelligen Zahlen wird der Multiplikator links und der Multiplikand rechts daneben geschrieben. Nullen am Ende des Multiplikators werden sofort an das Ende des Multiplikanden geschrieben. Die letzte Zahl des Multiplikators wird unter die höchste Zahl des Multiplikanden geschrieben. Bei der Durchführung der Multiplikation wird von links begonnen.
Als Beispiel sei hier als Multiplikator die Zahl 3210 und als Multiplikand die Zahl 92 gewählt. Die Aufgabenstellung lautet also 92•3210.
| 1.) Multiplikator 3210 und Multiplikand 92 werden platziert | (2.) 9•3 = 27 (wird notiert) | (3.) 9•2 = 18 (wird notiert) | (4.) 9•1 = 9 (wird notiert) | (5.) 9 wird getilgt. 32 und die 1 rücken nach rechts | (6.) 2•3 = 6 (wird notiert) | (7.) 2•2 = 4 (wird notiert) | (8.) 2•1 = 2 (wird notiert) | (9.) 2 wird getilgt. 32 und die 1 rücken nach rechts | (10.) Multiplikation mit 0 ergibt 0 |
|---|
| 32920 | 32920 | 32920 | 32920 | 3220 | 3220 | 3220 | 3220 | 320 | |
| 1__ | 1__ | 1__ | 1__ | 1_ | 1_ | 1_ | 1_ | 1 | |
| | 7____ | 78___ | 789__ | 789__ | 789__ | 789__ | 7892_ | 7892_ | 78920 |
| | 2_____ | 21____ | 21____ | 21____ | 216___ | 2164__ | 2164__ | 2164__ | 2164__ |
Anschließend sind die beiden übereinander geschriebenen Zahlen, also 78920 und 216400 (!) zu addieren, was nach dem beschriebenen Verfahren der Addition durchgeführt wird. Das Ergebnis ist 295320.
2.5. Division mehrstelliger natürlicher Zahlen
Die Division setzt die Kenntnis der Multiplikationstafel und der Bildung von Differenzen zu den Zahlen von 10 bis 90 voraus. Als Rechenbeispiel sei die Aufgabenstellung 1111101 : 707 vorgegeben. Zur Durchführung schreibt man Dividend und Divisor untereinander.
| | (1.) Aufgabenstellung: 1111101 : 707 | (2.) 10 : 7 = 1 (platziert). 10 − 7 = 3. Tilge 1 und 7, füge 3 hinzu | (3.) 3 wird addiert und getilgt | (4.) 7 x 1 = 7. 10 − 7 = 3. Tilge 1 und 7. Notiere 3 (zu addieren) | (5.) 3 wird addiert und getilgt | (6.) Notiere Divisor erneut | (7.) 40 : 7 = 5 (platziert). 40 − 35 = 5. Tilge 4 und 7. Notiere 5 (zu addieren) | (8.) 5 wird addiert und getilgt | (9.) 7 x 5 = 35. 40 − 35 = 5. Tilge 4 und 7. Notiere 5 (zu addieren) | (10.) 5 wird addiert und getilgt | (11.) Notiere Divisor erneut |
|---|
| Quotient | | 1_____ | 1_____ | 1_____ | 1_____ | 1_____ | 15____ | 15____ | 15____ | 15____ | 15____ |
| Dividend | 1111101 | 111101 | 411101 | 401101 | 404101 | 404101 | 04101 | 54101 | 50101 | 50601 | 50601 |
| Divisor | 707___ | 307___ | 7___ | 3___ | | 707__ | 507__ | 7__ | 5__ | | 707_ |
3. Durchführung astronomischer Berechnungen
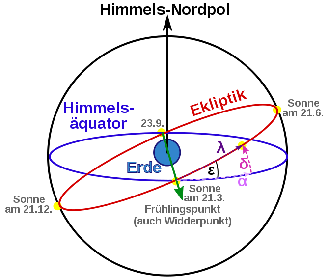
Die tibetische Astronomie beschäftigte sich insbesondere mit der Berechnung der Positionen – astronomisch Längen genannt – des Mondes, der Sonne und der Planeten Venus, Merkur, Mars, Jupiter und Saturn. Hierbei ist im geozentrischen Weltbild der Tibeter die Sonne ein Planet. Die tibetische Astronomie teilte unter anderem die Ekliptik, also den Großkreis, der durch die Projektion der scheinbaren Bahn der Sonne in Verlauf eines Jahres auf der Himmelskugel entsteht, in 27 Teile ein, die von 0 bis 26 gezählt wurden. Diese Teile eines Kreises, häufig Mondstationen oder Mondhäuser genannt, werden im Tibetischen als rgyu-skar „Sterne, auf denen man (d.s. die Planeten) geht“ bezeichnet. Mathematisch handelt es sich hierbei um ein Winkelmaß bzw. um ein Bogenmaß. Die Winkelmaßeinheit rgyu-skar wurde in 60 chu-tshod unterteilt. Eine chu-tshod wurde in 60 chu-srang unterteilt. Eine chu-srang bestand aus 6 dbugs, die wiederum in 67 cha-shas „Teile“ unterteilt wurden. Es wird deutlich, dass mit diesem System von Winkelmaßen die Länge eines Planeten sehr genau bestimmt werden konnte.
Die Aufgabenstellung, die hier als Beispiel gewählt wird, ist die Berechnung der mittleren Länge der Sonne (= y) am Ende des fünften synodischen Monats (x = 5) eines Jahres. Dazu wird die durchschnittliche Veränderung der Länge der Sonne pro synodischen Monat benötigt. Diese beträgt a = 2 (rgyu-skar) 10 (chu-tshod) 58 (chu-srang) 1 (dbugs) 17 (cha-shas). Außerdem wird die Länge der Sonne zum Jahresanfang benötigt. Diese sei hier mit b = 25 (rgyu-skar) 8 (chu-tshod) 10 (chu-srang) 4 (dbugs) 32 (cha-shas) angegeben.
In der Sprache der klassischen Algebra – die dem tibetischen Astronomen unbekannt war – stellt sich die Aufgabenstellung mit der linearen Gleichung y = a • x + b dar. Die konkrete Ausrechnung bleibt dabei angesichts des komplizierten Stellenwertsystems als Aufgabenstellung bestehen.
In tibetischen Lehrbüchern der Astronomie wird die Durchführung dieser Rechnung als Programmtext für den Sandabakus wie folgt dargestellt, wobei hier zum leichteren Verständnis die Zahlenwerte in Klammern ergänzt wurden:
Platziere die Zahl der vergangenen synodischen Monate (=x) auf fünf Stellen.
Von oben multipliziere nacheinander mit (a=) „Auge“ (2), „Himmelsrichtung“ (10), „Schlangengott Sinnesorgan“ (58), „Körper“ (1), „Mond Planet“ (17).
Von oben addiere nacheinander (b=) „Sosein“ (25), „Schatz“ (8), „Null Körper“ (10), „Veden“ (4), „Zähne“ (32).
Nach oben Umrechnung durch die Stellenwerte „Berg Geschmack“ (67), „Jahreszeit“ (6), „Himmel Geschmack“ (60), „Null Zwischenhimmelsrichtung“ (60), „Rad“ (27).
Der Rest, nach Löschen der höchsten Stelle, ist (=y) die mittlere Länge der Sonne.
Für die Durchführung der Rechnung auf dem Sandabakus ergibt sich die folgende Verfahrensweise. Hierzu sei nochmals darauf hingewiesen, dass auf dem Sandabakus immer nur eine Spalte mit Zahlen vorhanden ist, die durch Wegwischen und Ersetzen von Zahlen verändert wird:
| Stellenwert | (1.) Platziere vergangene Monate (x) auf fünf Stellen | (2.) Von oben multipliziere nacheinander mit (a=) 2, 10, 58, 1, 17 | (2a.) Ergebnis der Multiplikation | (3.) Von oben addiere nacheinander (b=) 25, 8, 10, 4, 32 | (3a.) Ergebnis der Addition | (4.) Nach oben Umrechnung durch den Stellenwert 67 | (4a.) Umrechnung durch den Stellenwert 6 | (4b.) Umrechnung durch den Stellenwert 60 | (4c.) Umrechnung durch den Stellenwert 60 | (4c.) Umrechnung durch den Stellenwert 27 | (5.) Die Reste sind die mittlere Länge der Sonne (y) |
|---|
| 27 | 5 | 5•2 | 10 | 10+25 | 35 | 35 | 35 | 35 | 35 | (35+1):27 | 9 |
| 60 | 5 | 5•10 | 50 | 50+8 | 58 | 58 | 58 | 58 | (58+5):60 | 3 | 3 |
| 60 | 5 | 5•58 | 290 | 290+10 | 300 | 300 | 300 | (300+1):60 | 1 | 1 | 1 |
| 6 | 5 | 5•1 | 5 | 5+4 | 9 | 9 | (9+1):6 | 4 | 4 | 4 | 4 |
| 67 | 5 | 5•17 | 85 | 85+32 | 117 | 117:67 | 50 | 50 | 50 | 50 | 50 |
4. Rechnen mit Zahlen im Sexagesimalsystem
Die Zahlenwerte einer Größenangabe, bei der man nicht dem Dezimalsystem folgt, werden auf dem Sandabakus untereinander geschrieben. Die an der jeweiligen Stelle notierte Zahl ist in der tibetischen Astronomie bzw. beim Rechnen auf dem Sandabakus stets eine ganze Zahl. Die Stellen sind stets übereinander platziert, also zum Beispiel für 3 rgyu-skar, 26 chu-tshod, 5 chu-srang und 4 dbugs:
Die Stellenwerte sind in diesem Beispiel (von oben nach unten) 27, 60, 60 und 6. Man folgte also im Wesentlichen dem Sexagesimalsystem. Die Stellenwerte wurden in Tibet nicht gesondert notiert.
Um solche Zahlen im Folgenden raumsparender wiederzugeben, werden die Zahlgrößen in eckigen Klammern mit Kommata getrennt notiert und die Stellenwerte dahinter durch einen Schrägstrich getrennt in runden Klammern angegeben. Der vorstehende Zahlenwert wird also als [3,26,5,4]/(27,60,60,6) wiedergegeben. Allgemein gesprochen werden im Folgenden solche meist fünfstellige Zahlen als
- [a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5)
geschrieben, wobei an Ganze Zahlen und stn die Stellenwerte sind.
4.1. Addition und Subtraktion
Für die Addition zweier mehrstelliger Zahlen verfährt man nach der Regel:
[a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5) + [b1,b2,b3,b4,b5]/(st1,st2,st3,st4,st5) =
[a1 + b1,a2 + b2,a3 + b3,a4 + b4,a5 + b5]/(st1,st2,st3,st4,st5).
Falls einzelne Summen größer als der Stellenwert sind, wird nach dem unten (siehe Multiplikation und Umrechnung auf Stellenwerte) beschriebenen Verfahren umgerechnet.
Bei der Subtraktion verfährt man analog:
[a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5) - [b1,b2,b3,b4,b5]/(st1,st2,st3,st4,st5) =
[a1 − b1,a2 − b2,a3 − b3,a4 − b4,a5 - b5]/(st1,st2,st3,st4,st5).
Falls der abzuziehende Betrag (Subtrahend) größer als der zu vermindernde Betrag (Minuend) ist, wird vor der Subtraktion der über dem Minuend stehende Betrag um eins vermindert und der Stellenwert zum Minuenden addiert. Tritt dies bei der höchsten Stelle auf, wird diese einfach um den Stellenwert erhöht.
4.2. Multiplikation und Umrechnung auf Stellenwerte
Die Multiplikation einer mehrstelligen Größenangabe mit einer Ganzen Zahl c gestaltet sich noch relativ einfach. Hier lautet die allgemeine den tibetischen Mathematikern geläufige Lösung der Aufgabenstellung:
c • [a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5) =
[ ]/(st1,st2,st3,st4,st5).
]/(st1,st2,st3,st4,st5).
Wesentlich schwieriger gestaltete sich für die Tibetischen Mathematiker die Lösung der Multiplikation von zwei mehrstelligen Größenangaben, also die Lösung der Aufgabe
[a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5) • [b1,b2,b3,b4,b5]/(st1,st2,st3,st4,st5),
wobei es vorkommen konnte, dass auch die Stellenwerte der zu multiplizierenden Zahlengrößen verschieden waren.
Solche Aufgabenstellungen ergaben sich durch zwei Umrechnungsfaktoren. Der erste dieser beiden Werte (A) gibt das Verhältnis des mittleren solaren Monats oder Zodiak-Tages zum mittleren synodischen Monat oder mittleren lunaren Tag an und wird wie folgt notiert:
[1,2]/(-,65)
Es ist anzumerken, dass dieser Faktor, als Bruch geschrieben, mit
A = 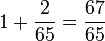
gleichzusetzen ist.
Der zweite dieser Umrechnungsfaktoren (B) gibt das Verhältnis des mittleren lunarem Tages zum mittleren natürlichen Tag an und wird wie folgt notiert:
1 – [0,1,1]/(-,64,707).
Als Bruch geschrieben entspricht dies B = 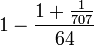 .
.
Multipliziert man den Umrechnungsfaktor A mit der Umlaufzeit der Sonne in Zodiak Tagen, d.i. mit 360, so erhält man mit Umlaufzeit der Sonne in lunaren Tagen. Die relativ einfache Umrechnung mit dem Sandabakus auf die Stellenwerte der Zeiteinheit lunarer Tag ergibt dann Folgendes:
- [360 • 1, 360 • 2]/(-,65) =
- [371, 4, 40]/(-, 60,65) =
- [371,4, 2400]/(-,60, 65 • 60) =
- [371, 4, 36, 60]/(-,60,60,65) =
- [371, 4, 36, 360]/(-,60,60,65 • 6) =
- [371 ,4, 36, 5, 35]/(-,60,60,6, 65) =
- [371 ,4, 36, 5, 7]/(-,60,60,6, 13).
Dies ist die Umlaufzeit der Sonne in lunaren Tagen. Das Verfahren der Umrechnung auf Stellenwerte selbst entspricht dem Erweitern von Brüchen. In der Sprache der modernen Mathematik entspricht diese Rechnung
360 • a = 360 • 67/65 = 371,107962 lunare Tage.
Die vorstehende Rechnung liefert gleichzeitig ein Beispiel für die Division einer mehrstelligen Zahlgröße durch eine Ganze Zahl, da in ihr die die Aufgabenstellung
[720,0,0,0]/(60,60,6) : 65 enthalten ist.
Zur Errechnung der Umlaufzeit der Sonne in natürlichen Tagen hat man nun die Umlaufzeit der Sonne in lunaren Tagen mit B zu multiplizieren, was für den tibetischen Astronomen die Aufgabenstellung
[371,4,36,5,7]/(-,60,60,6,13) • (1- [0,1,1]/(-,64,707)) =
[371,4,36,5,7]/(-,60,60,6,13) - [371,4,36,5,7]/(-,60,60,6,13) • [0,1,1]/(-,64,707)
ergab.
Mit
[371,4,36,5,7]/(-,60,60,6,13) • [0,1,1]/(-,64,707)
liegt die Aufgabenstellung der Multiplikation von zwei Zahlen mit unterschiedlichen Stellenwerten vor.
Die tibetischen Astronomen lösten solche Aufgabenstellungen dadurch, dass sie das Problem auf die oben beschriebene Aufgabe
c • [a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5) = [ ]/(st1,st2,st3,st4,st5)
]/(st1,st2,st3,st4,st5)
zurückführten, wobei c eine Ganze Zahl ist.
Im vorliegenden Fall wurde dazu der Betrag der Umlaufzeit der Sonne von [371,4,36,5,7]/(-,60,60,6,13) nicht nur auf die kleinste Einheit 13, sondern auf die winzige Zeiteinheit 13 • 707 Teile der dbugs umgerechnet.
Generell entspricht dies zum Beispiel der Umrechnung einer Zeitangabe von Tagen, Stunden, Minuten und Sekunden in die Größeneinheit Sekunde, wie etwa, dass 1 Tag + 0 Stunden + 0 Minuten + 0 Sekunden gleich 86400 Sekunden ist.
Im vorliegenden Fall ist das Ergebnis der Umrechnung 73668268800 und die Aufgabenstellung läuft auf die Rechenaufgabe
73668268800 –73668268800 • [0,1,1]/(-,64,707) = 73668268800 – [0, 73668268800 • 1, 73668268800 • 1]/(-, 64,707) hinaus.
Das Ergebnis dieser Rechnung beläuft sich auf 72515574000 und ist die Umlaufzeit der Sonne in 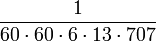 natürlichen Tagen.
natürlichen Tagen.
Nach tibetischer Darstellung auf dem Sandabakus ergibt dies für die Umlaufzeit der Sonne in natürlichen Tagen somit den Betrag
[0, 0, 0, 0, 0, 72515574000]/(-,60,60,6,13,707) bzw. nach Umrechnung
[365, 16, 14, 1, 12, 121]/(-,60,60,6,13,707).
4.3. Division
Die Division einer mehrstelligen Zahlengröße durch eine Ganze Zahl c wird entsprechend
[a1:c,a2:c,a3:c,a4:c,a5:c]/(st1,st2,st3,st4,st5)
durchgeführt. Dabei beginnt man an der obersten Stelle. Die Reste der Division der jeweiligen höheren Stellen werden dabei mit dem Stellenwert der nachfolgenden Stelle multipliziert und vor der Division dieser Stelle mit dem Zahlenwert dieser Stelle addiert.
Die Aufgabenstellung erweist sich als schwieriger, wenn der Divisor auch eine mehrstellige Zahlengröße ist, wie in:
[a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5) : [b1,b2,b3,b4,b5]/(st1,st2,st3,st4,st5).
Hierbei konnte es vorkommen, dass auch die Stellenwerte des Divisors von denen des Dividenden verschieden waren. Da die Anzahl solcher Aufgabenstellungen begrenzt war, versuchten die tibetischen Astronomen in diesen Fällen, die Aufgabe auf eine Multiplikation zurückzuführen. Dies erfolgte dadurch, dass man bei einem Divisor C den Kehrwert ermittelte und das Ergebnis mit dem Dividenden multiplizierte.
Hierzu zwei Beispiele:
1. Der Divisor sei B = 1 – [0,1,1]/(-,64,707).
In diesem Fall ermittelte man für die Größe [1, 1, 1, 1]/(-,63,696,11135). Mit dieser Größe als Faktor wurde sodann der Dividend multipliziert.
2. Der Divisor sei A = [1,2]/(-,65). In diesem Fall ermittelte man für den Wert 1 – [0, 2]/(-,67), mit dem dann der Dividend zu multiplizieren war.
5. Literatur
Dieter Schuh: Studien zur Geschichte der Mathematik und Astronomie in Tibet, Teil 1, Elementare Arithmetik. Zentralasiatische Studien des Seminars für Sprach- und Kulturwissenschaft Zentralasiens der Universität Bonn, 4, 1970, S. 81–181
Dieter Schuh: Untersuchungen zur Geschichte der Tibetischen Kalenderrechnung. Wiesbaden 1973
Autor Dieter Schuh, 2010. Bildnachweis: Ekliptik S. fonsi http://commons.wikimedia.org/wiki/File:Ecliptic.svg?uselang=de .





